Архитектурная акустика/Интеграл Релея (версия Кулигина): различия между версиями

Материал из CAMaaS preliminary wiki
Перейти к навигации Перейти к поиску
Строка 10: Строка 10:
на сфере <math>r=0</math>, где:
на сфере <math>r=0</math>, где:
* <math>\varphi(\theta, \varphi, r)</math> - потенциал колебательной скорости в точке, заданной в сферической системе координат, в которой <math>\theta = 0, \varphi = 0, r = 1</math> - единичный вектор сонаправленный главной оси источника.
* <math>\varphi(\theta, \varphi, r)</math> - потенциал колебательной скорости в точке, заданной в сферической системе координат, в которой <math>\theta = 0, \varphi = 0, r = 1</math> - единичный вектор сонаправленный главной оси источника.
* <math>\sigma</math> - [[Архитектурная акустика/Поверхность|поверхность]] или ее часть, которая которая колеблется как поршень.
* <math>\sigma</math> - [[Архитектурная акустика/Поверхность|поверхность]] или ее часть, которая колеблется как поршень.
* <math>d\sigma</math> - малый элемент поверхности в окрестности некоторой точки <math>(x, y)</math>, принадлежащей поверхности и заданной в системе координат поверхности, в которой аппликата сонаправлена главной оси источника.
* <math>d\sigma</math> - малый элемент поверхности в окрестности некоторой точки <math>(x, y)</math>, принадлежащей поверхности и заданной в системе координат поверхности, в которой аппликата сонаправлена главной оси источника.
* <math>\frac{\partial\varphi}{\partial\stackrel{\to}{n}}</math> - проекция градиента потенциала колебательной скорости <math>\varphi</math> на нормаль <math>\stackrel{\to}{n}</math> к <math>\sigma</math>.
* <math>\frac{\partial\varphi}{\partial\stackrel{\to}{n}}=v_n</math> - проекция градиента потенциала колебательной скорости <math>\varphi</math> на нормаль <math>\stackrel{\to}{n}</math> к <math>\sigma</math>. Фактически является нормальной составляющей колебательной скорости источника
* <math>i = \sqrt{-1}</math>.
* <math>i = \sqrt{-1}</math>.
* <math>r'\left(\theta, \varphi, r\right)=\sqrt{\left(r\sin\varphi\cos\theta-x\right)^2 + \left(r\sin\varphi\sin\theta-y\right)^2+\left(r\cos\varphi\right)^2}</math>.
* <math>r'\left(\theta, \varphi, r\right)=\sqrt{\left(r\sin\varphi\cos\theta-x\right)^2 + \left(r\sin\varphi\sin\theta-y\right)^2+\left(r\cos\varphi\right)^2}</math>.
Строка 18: Строка 18:


=Алгоритм=
=Алгоритм=
#Задаются полигоны всех поверхностей помещения.
#Разбитие всех полигонов поверхностей помещения на элементы (источники) с некоторыми линейными размерами, которое зависит от частоты рассчитываемого тона.
#Задаются контрольные плоскости вывода результата.
#<math>SC' \gets SC</math> - временное множество источников, для хранения первичных и вторичных источников SC'
#Для всех источников <math>s\in SC'</math> (цикл):
#<math>SC' \gets SC'  \setminus\left\{s'_i\right\}</math>
##Из каждого источника излучается луч во все остальные отражающие элементы <math>PC-1</math>при условии, что источник SC излучает только в пределах своего телесного угла <math>\Omega>2\pi</math>.
## Для каждого луча <math>r_i\in s</math> (цикл):
###Если интенсивность луча <math>r_i</math>  меньше какого-либо порогового значения, то перейти на шаг 7.2, иначе:
####Каждый излученный луч проверяется на пересечение с другими полигонами, т.е. на наличие тени.
####Каждый излученный луч пересекается с контрольной плоскостью. Фиксируется характеристика в комплексном виде и записывается в буфер, связанный с точкой.
####Луч пересекает отражающий элемент, возбуждая колебания с определенной фазой в зависимости от того, с какой фазой на него упал луч. В формуле (1) имеем: <math>\frac{\partial\varphi}{\partial\stackrel{\to}{n}}=(grad \varphi_1,\stackrel{\to}{n})=-ike^{i(\omega t-\stackrel{\to}{k}\stackrel{\to}{r_1})}\cos \widehat{\stackrel{\to}{r_1},\stackrel{\to}{n}}</math>
####Каждый отражающий элемент становится источником <math>s'_i</math> с определенными характеристиками (объемной скоростью колебаний), т.е. <math>SC' \gets SC' \cup\left\{s'_i\right\}</math>.
#Конец цикла


Предусловия:
Предусловия:
# <tt>M</tt> - [[Архитектурная акустика/Среда распространения звука|Среда распространения звука]];
# <tt>N</tt> - порядок источника, принимает значения от 1 для первичного источника и до бесконечности
# <tt>SC = M.Множество [[Архитектурная акустика/Первичный источник|источников]]()</tt>;
# <tt>SC = M.Множество [[Архитектурная акустика/Первичный источник|источников]]()</tt>;
# <tt>PC = M.Множество [[Архитектурная акустика/Объемный геометрический объект|отражающих элементов]]()</tt>
# <tt>PC = M.Множество [[Архитектурная акустика/Объемный геометрический объект|отражающих элементов]]()</tt>

Версия 15:18, 16 июня 2016

Архитектурная акустика\Интеграл Релея (версия Кулигина)

Модель распространения звука в помещении, в которой каждая поверхность представлена в виде системы плоских колеблющихся поршней. Каждый такой поршень при попадании на него звукового луча оказывается вторичным источником звука.

Является вариантом реализации модели расчета акустического поля, в котором, в отличие от исходной версии вся поверхность помещения разбивается на элементы малой площади. В модели анализируется влияние каждого имеющегося источника звука на каждый возможный элемент излучения . Каждый источник Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s оказывает влияние на каждый элемент Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): d\sigma , если только Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): d\sigma не находится в тени источника , и влияние этого источника на поверхность не падает ниже пренебрежимого уровня звука модели среды распространения. Если влияние действительно имеется, элемент Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): d\sigma сам становится источником отраженного звука. Направленность такого источника рассчитывается с помощью интеграла Релея:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi\left(\theta, \varphi, r\right) = \frac{1}{2\pi}\iint\limits_{\sigma}\frac{\partial\varphi_1}{\partial\stackrel{\to }{n}}\frac{e^{-i k r}}{r}d\sigma

на сфере Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r=0 , где:

  • Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi(\theta, \varphi, r) - потенциал колебательной скорости в точке, заданной в сферической системе координат, в которой Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta = 0, \varphi = 0, r = 1 - единичный вектор сонаправленный главной оси источника.
  • Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \sigma - поверхность или ее часть, которая колеблется как поршень.
  • Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): d\sigma - малый элемент поверхности в окрестности некоторой точки , принадлежащей поверхности и заданной в системе координат поверхности, в которой аппликата сонаправлена главной оси источника.
  • Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \frac{\partial\varphi}{\partial\stackrel{\to}{n}}=v_n - проекция градиента потенциала колебательной скорости Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi на нормаль Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \stackrel{\to}{n} к Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \sigma . Фактически является нормальной составляющей колебательной скорости источника
  • Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i = \sqrt{-1} .
  • Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r'\left(\theta, \varphi, r\right)=\sqrt{\left(r\sin\varphi\cos\theta-x\right)^2 + \left(r\sin\varphi\sin\theta-y\right)^2+\left(r\cos\varphi\right)^2} .


Алгоритм

  1. Задаются полигоны всех поверхностей помещения.
  2. Разбитие всех полигонов поверхностей помещения на элементы (источники) с некоторыми линейными размерами, которое зависит от частоты рассчитываемого тона.
  3. Задаются контрольные плоскости вывода результата.
  4. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): SC' \gets SC - временное множество источников, для хранения первичных и вторичных источников SC'
  5. Для всех источников Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s\in SC' (цикл):
  6. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle SC' \gets SC' \setminus\left\{s'_i\right\}}
    1. Из каждого источника излучается луч во все остальные отражающие элементы Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle PC-1} при условии, что источник SC излучает только в пределах своего телесного угла Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Omega>2\pi} .
    2. Для каждого луча Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_i\in s} (цикл):
      1. Если интенсивность луча Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r_i меньше какого-либо порогового значения, то перейти на шаг 7.2, иначе:
        1. Каждый излученный луч проверяется на пересечение с другими полигонами, т.е. на наличие тени.
        2. Каждый излученный луч пересекается с контрольной плоскостью. Фиксируется характеристика в комплексном виде и записывается в буфер, связанный с точкой.
        3. Луч пересекает отражающий элемент, возбуждая колебания с определенной фазой в зависимости от того, с какой фазой на него упал луч. В формуле (1) имеем: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \frac{\partial\varphi}{\partial\stackrel{\to}{n}}=(grad \varphi_1,\stackrel{\to}{n})=-ike^{i(\omega t-\stackrel{\to}{k}\stackrel{\to}{r_1})}\cos \widehat{\stackrel{\to}{r_1},\stackrel{\to}{n}}
        4. Каждый отражающий элемент становится источником Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s'_i с определенными характеристиками (объемной скоростью колебаний), т.е. .
  1. Конец цикла


Предусловия:

  1. N - порядок источника, принимает значения от 1 для первичного источника и до бесконечности
  2. SC = M.Множество источников();
  3. PC = M.Множество отражающих элементов()
  4. PlC = M.Множество контрольных точек() - множество плоскостей вывода результатов.
  5. расстояние(точка1, точка2) - функция расстояния между двумя точками.

Течение алгоритма:

  1. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): SC' \gets SC - изменяемое множество всех источников.
  2. Если SC' пусто.
    1. Завершение алгоритма.
  3. Для всех источников Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s\in SC'
    2. Пусть множество лучей: RS = s.Излучаемый звук()
    3. Для всех лучей Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r\in RS
      1. Если r.Интенсивность() > M.Пренебрежимый уровень звука()
        1. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): PlC' = \left\{pl_i\right\}\subset PlC: \exists pt = pl_i\cap r\land расстояние(r.Позиция(), pt)Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leq расстояние(r.Позиция(), r.Ближайшая поверхность(PC)Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \cap r) - множество плоскостей вывода результатов, с которыми существуют пересечения луча Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r , и которые не находятся в тени.
        2. Для всех плоскостей Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): pl\in PlC'
          1. Точка пересечения Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): pt \gets pl\cap r
          2. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I\gets r.Интенсивность(расстояние(r.Позиция(), pt))
          3. Если M.Пренебрежимый уровень звука()
            1. pl.Зарегистрировать звук(pt, I, r.Частота())
        3. Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \exists f = r.Ближайшая поверхность(PC)
          1. Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P\gets f\cap r
          2. Если r.Интенсивность(расстояние(r.Позиция(), P)) > M.Пренебрежимый уровень звука()
            1. Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): f' - плоская круглая поверхность диаметром, равным длине волны звука, ассоциированного с лучом Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r (см. r.Частота()), вокруг точки пересечения P.
            2. s' = Вторичный источник на основе интеграла РелеяНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (f\cap f', r, f \cap r)
            3. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): SC' \gets SC' \cup \left\{s'\right\} - дополнение множества SC' новым вторичным источником s'
  4. Переход на шаг 2.
Граф параллельного выполнения алгоритма. Для краткости используются сокращенные записи методов сущностей архитектурной акустики: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I\left(r\right)\sim r .Интенсивность(); Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I\left(r, pt\right)\sim r .Интенсивность(расстояние(r.Позиция(), pt)); Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I_0\sim M .Пренебрежимый уровень звука(); Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega\left(r\right)\sim r .Частота(); Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): pl.Reg\left(pt, I, \omega\right)\sim pl .Зарегистрировать звукНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \left(pt, I, \omega\right) ;

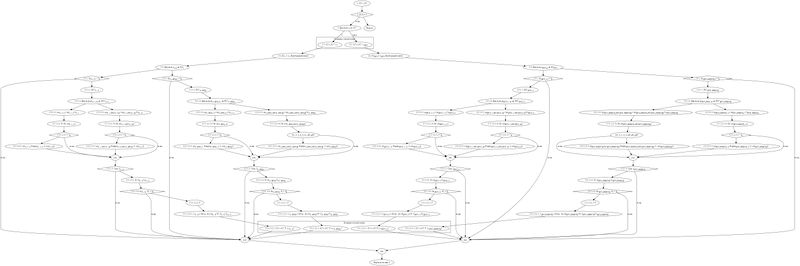
Свойства алгоритма

Пусть - множество первичных источников (см. свойство множество источников() среды распространения звука).

Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R_s = \sum\limits_{i=1}^{|S|}|s_i. Излучаемый звук()Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): | - суммарное количество лучей от всех первичных источников.

Тогда сложность: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): O\left(R_s^{\frac{\max\limits_{i=1,N_s}\left(I(s_i)\right)}{I_0}}\right) , где Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I\left(s\right) = \max\limits_{\forall\omega\in B\left(s\right)} (s.Интенсивность(0, 0, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega )) - максимальное значение характеристики звука, излучаемого источником Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s по частотам Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): B\left(s\right) , на которых определена его АЧХ, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I_0 - пренебрежимый уровень звука (свойство среды распространения).

Источник — http://51.250.0.107/w/index.php?title=Архитектурная_акустика/Интеграл_Релея_(версия_Кулигина)&oldid=2881