Архитектурная акустика/Интеграл Релея

Архитектурная акустика\Интеграл Релея

Модель распространения звука в помещении, в которой каждая поверхность представлена в виде системы плоских колеблющихся поршней. Каждый такой поршень при попадании на него звукового луча оказывается вторичным источником звука.

Направленность такого источника рассчитывается с помощью интеграла Релея:

$\varphi\left(\theta, \varphi, r\right) = \frac{V_0 e^{i\cdot\left(\omega t-\varphi\right)}}{2\pi}\iint\limits_{S}{\frac{e^{-ikr'\left(\theta, \varphi, r\right)}}{r'\left(\theta, \varphi, r\right)}dS}$,

где:

• $\varphi(\theta, \varphi, r)$ - потенциал колебательной скорости в точке, заданной в сферической системе координат, в которой $\theta = 0, \varphi = 0, r = 1$ - единичный вектор сонаправленный главной оси источника.
• $S$ - поверхность или ее часть, которая которая колеблется как поршень.
• $dS$ - малый элемент поверхности в окрестности некоторой точки $(x, y)$, принадлежащей поверхности и заданной в системе координат поверхности, в которой аппликата сонаправлена главной оси источника.
• $V_0$ - амплитуда колебательной скорости.
• $\omega$ - круговая частота колебаний поршня.
• $t$ - время измерения направленности.
• Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi - начальная фаза колебаний.
• Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i = \sqrt{-1} .
• Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r'\left(\theta, \varphi, r\right)=\sqrt{\left(r\sin\varphi\cos\theta-x\right)^2 + \left(r\sin\varphi\sin\theta-y\right)^2+\left(r\cos\varphi\right)^2} .

Алгоритм

Предусловия:

1. M - Среда распространения звука;
2. SC = M.Множество источников();
3. PC = M.Множество отражающих элементов()
4. PlC = M.Множество контрольных точек() - множество плоскостей вывода результатов.
5. расстояние(точка1, точка2) - функция расстояния между двумя точками.

Течение алгоритма:

1. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): SC' \gets SC - изменяемое множество всех источников.
2. Для всех источников Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s\in SC'
   1. Пусть множество лучей: RS = s.Излучаемый звук()
   2. Для всех лучей Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r\in RS
      1. Если r.Интенсивность() > M.Пренебрежимый уровень звука()
         1. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): PlC' = \left\{pl_i\right\}\subset PlC: \exists pt = pl_i\cap r\land расстояние(r.Позиция(), pt)Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leq расстояние(r.Позиция(), r.Ближайшая поверхность(PC)Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \cap r) - множество плоскостей вывода результатов, с которыми существуют пересечения луча Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r , и которые не находятся в тени.
            1. Для всех плоскостей Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): pl\in PlC'
               1. Точка пересечения Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): pt \gets pl\cap r
               2. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I\gets r.Интенсивность(расстояние(r.Позиция(), pt))
               3. Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I > M.Пренебрежимый уровень звука()
                  1. pl.Зарегистрировать звук(pt, I, r.Частота())
         2. Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \exists f = r.Ближайшая поверхность(PC)
            1. Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P\gets f\cap r
            2. Если r.Интенсивность(расстояние(r.Позиция(), P)) > M.Пренебрежимый уровень звука()
               1. Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): f' - плоская круглая поверхность диаметром, равным длине волны звука, ассоциированного с лучом Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r (см. r.Частота()), вокруг точки пересечения P.
               2. s' = Вторичный источник на основе интеграла РелеяНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (f\cap f', r, f \cap r)
               3. $SC' \gets SC' \cup \left\{s'\right\}$ - дополнение множества SC' новым вторичным источником s'

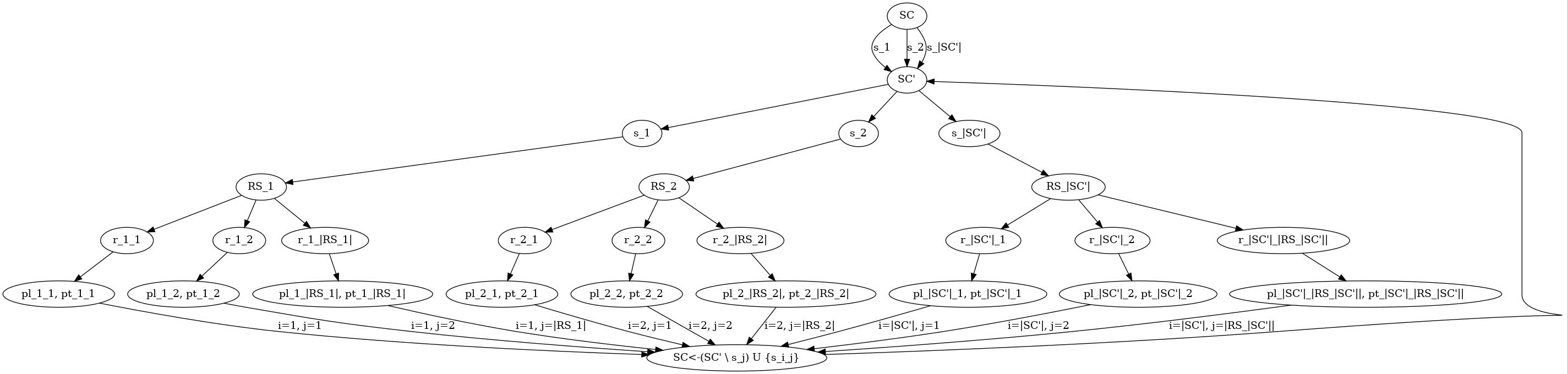
Свойства алгоритма

Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S - множество первичных источников (см. свойство множество источников() среды распространения звука).

Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R_s = \sum\limits_{i=1}^{|S|}|s_i. Излучаемый звук()Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): | - суммарное количество лучей от всех первичных источников.

Тогда сложность: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): O\left(R_s^{\frac{\max\limits_{i=1,N_s}\left(I(s_i)\right)}{I_0}}\right) , где Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I\left(s\right) = \max\limits_{\forall\omega\in B\left(s\right)} (s.Интенсивность(0, 0, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega )) - максимальное значение характеристики звука, излучаемого источником Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s по частотам Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): B\left(s\right) , на которых определена его АЧХ, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I_0 - пренебрежимый уровень звука (свойство среды распространения).