Распространение радиоволн ВЧ/Напряженность
Трехкомпонентный комплексный вектор который задается волновым элементом, порождаемым источником , в результате распространения и отражений в среде.
Вектор рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
Модель распространения
Пусть - дальняя зона, расстояние, на котором для источника снята начальная напряженность .
В результате распространения излученного элемента волны на расстояние напряженность поля падает в раз, становясь равной
- , где:
- - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны,
- - комплексное волновое число
Таким образом .
Здесь первая экспонента является коэффициентом поглощения среды на расстоянии , а
- погонным затуханием среды [дБ/м]
В частности, при отсутствии инерционности поляризации и намагничивания :
.
Тогда, в результате распространения волнового элемента на расстояние от источника в одной и той же изотропной среде, результирующая напряженность станет равной
- ,
где , и .
В более общем случае
- ,
где .
Модель отражения
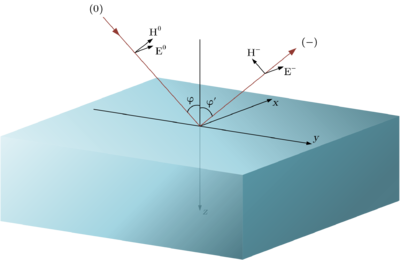
Пусть электрическая напряженность волнового элемента, падающего на плоскую поверхность с нормалью , задается некоторым комплексным вектором . Пусть эта поверхность является границей раздела двух сред.
- среды с четверкой параметров , в которой распространяется падающая волна, и
- среды с четверкой параметров , на границу которой падает волна.
Соответственно, - угол падения (и отражения), а угол - угол преломления.
Здесь:
- - комплексная диэлектрическая проницаемость, где
- - диэлектрическая проницаемость среды,
- - проводимость среды,
- - круговая частота волны,
- - угол диэлектрических потерь;
- - комплексная магнитная проницаемость, где
- - магнитная проницаемость среды,
- - угол магнитных потерь;
- - комплексное волновое число;
- - комплексное волновое сопротивление;
- согласно закону Снеллиуса, причем
- - коэффициент преломления соответствующей среды.
Тогда коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля) соответственно:
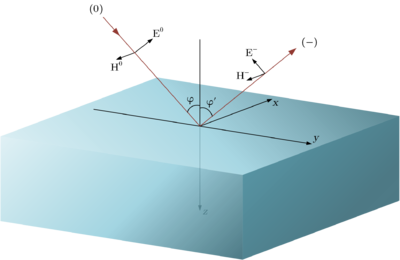
Пусть - вектор электрической напряженности падающей на поверхность волны, где - соответствующая матрица поворота, выраженный в системе координат такой, что ось абсцисс совпадает по направлению с - векторным произведением направляющего вектора луча и нормали поверхности, а ось аппликат - с .
Тогда вектор напряженности отраженной волны, в мировых координатах, равен
- ,
где
- - матрица поворота вектора напряженности на угол через нормаль вокруг ;
- ;
, , .
Таким образом, напряженность электрического поля волнового элемента в результате его отражений и прохождений в (различных изотропных) средах рассчитывается по формуле
- .
Метод реализации
Напряженность поля - реализуется трехкомпонентным комплексным вектором .
Состояние объекта, реализующего волновой элемент, задается:
- , где - расстояние в дальней зоне источника, на котором снято значение напряженности первичного источника;
- - круговая частота волнового элемента;
- - расстояние, пройденное в общем волновым элементом от первичного источника до его текущего расположения;
- - фазовый сдвиг, которому подвергся волновой элемент в результате прохождения им расстояния ;
- - матрица, реализующая отражение вектора напряженности.
Тогда напряженность волнового элемента после всех распространений и отражений будет
- .
Методы
- Изменить по пробегу(Пробег, Комплексное волновое число)
- Изменить по отражению(КДП_1*, КМП_1**, КДП_2, КМП_2, Вектор(Направление луча), Вектор(Нормаль грани))===
* - комплексная диэлектрическая проницаемость, ** - комплексная магнитная проницаемость.
 который задается волновым элементом, порождаемым
который задается волновым элементом, порождаемым  , в результате распространения и отражений в среде.
, в результате распространения и отражений в среде.
 рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
 - дальняя зона, расстояние, на котором для источника
- дальняя зона, расстояние, на котором для источника  .
.
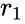 напряженность поля падает в
напряженность поля падает в  раз, становясь равной
раз, становясь равной
 , где:
, где: - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны,
- скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны, - комплексное волновое число
- комплексное волновое число



 .
.
 - погонным затуханием среды [дБ/м]
- погонным затуханием среды [дБ/м]
 :
:
 .
.
 от источника в одной и той же изотропной среде, результирующая напряженность станет равной
от источника в одной и той же изотропной среде, результирующая напряженность станет равной
 ,
, ,
,  и
и  .
.
 ,
, .
.
 , задается некоторым комплексным вектором
, задается некоторым комплексным вектором  . Пусть эта поверхность является границей раздела двух сред.
. Пусть эта поверхность является границей раздела двух сред.
 , в которой распространяется падающая волна, и
, в которой распространяется падающая волна, и , на границу которой падает волна.
, на границу которой падает волна. - угол падения (и отражения), а угол
- угол падения (и отражения), а угол  - угол преломления.
- угол преломления.
 - комплексная диэлектрическая проницаемость, где
- комплексная диэлектрическая проницаемость, где
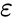 - диэлектрическая проницаемость среды,
- диэлектрическая проницаемость среды, - проводимость среды,
- проводимость среды, - круговая частота волны,
- круговая частота волны, - угол диэлектрических потерь;
- угол диэлектрических потерь; - комплексная магнитная проницаемость, где
- комплексная магнитная проницаемость, где
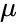 - магнитная проницаемость среды,
- магнитная проницаемость среды, - угол магнитных потерь;
- угол магнитных потерь; - комплексное волновое сопротивление;
- комплексное волновое сопротивление; согласно
согласно  - коэффициент преломления соответствующей среды.
- коэффициент преломления соответствующей среды.

 - вектор электрической напряженности падающей на поверхность волны, где
- вектор электрической напряженности падающей на поверхность волны, где  - соответствующая матрица поворота, выраженный в системе координат такой, что ось абсцисс совпадает по направлению с
- соответствующая матрица поворота, выраженный в системе координат такой, что ось абсцисс совпадает по направлению с  - векторным произведением направляющего вектора луча
- векторным произведением направляющего вектора луча 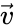 и нормали
и нормали  ,
, - матрица поворота вектора напряженности на угол
- матрица поворота вектора напряженности на угол  через нормаль вокруг
через нормаль вокруг  ;
; ;
; ,
,
 ,
,
 .
.
 отражений и
отражений и  прохождений в (различных изотропных) средах рассчитывается по формуле
прохождений в (различных изотропных) средах рассчитывается по формуле
 .
. .
.
 , где
, где 
 - расстояние, пройденное в общем волновым элементом от первичного источника до его текущего расположения;
- расстояние, пройденное в общем волновым элементом от первичного источника до его текущего расположения; - фазовый сдвиг, которому подвергся волновой элемент в результате прохождения им расстояния
- фазовый сдвиг, которому подвергся волновой элемент в результате прохождения им расстояния  ;
; - матрица, реализующая отражение вектора напряженности.
- матрица, реализующая отражение вектора напряженности. .
.