Шаблон:Распространение радиоволн ВЧ/Реализация/encompassing aperture t::unify/Алгоритм

Пусть объединяются два сектора сферы, релизуемые классом классом encompassing_aperture_t - Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Omega_1=\left\langle\vec{c}_1, \alpha_1\right\rangle} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Omega_2=\left\langle\vec{c}_2, \alpha_2\right\rangle} , где Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_i} - вектор направления на центральную точку Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i -го сектора (возвращаемый методом encompassing_aperture_t::central_point), а Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \alpha _{i}} - соответствующий ангулярный радиус (возвращаемый методом encompassing_aperture_t::radius).

Сектор encompassing_aperture_t

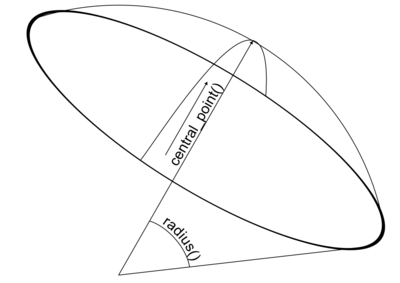
В результате объединения создается новый сектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Omega_{12}=\left\langle\vec{c}_{12}, \alpha_{12}\right\rangle = \Omega_1\cup\Omega_2} .

Вектора Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_i} могут быть либо нулевыми либо единичными. Сектор с нулевым вектором направления считается нейтральным по операции объединения, т.е. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\langle\vec{0}, \alpha_1\right\rangle\cup\Omega=\Omega\cup\left\langle\vec{0}, \alpha_2\right\rangle = \Omega} .

Далее рассматривается случай, в котором Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left|\vec{c}_1\right|=\left|\vec{c}_2\right|=1} .

Поскольку направленные отрезки Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_2} исходят из одной точки - центра сферы, оба отрезка принадлежат одной плоскости, причем эта плоскость является диаметральным сечением сферы. Поэтому задача поиска объединяющего сектора, то есть вектора ${\vec {c}}_{12}$ и ангулярного радиуса Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha_{12}} , становится двумерной.

Диаметральное сечение сферы, которому принадлежат вектора Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_2} . Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_1\nparallel\vec{c'}_2} , то вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_{12}} , задающий направление на центральную точку объединяющего сектора, будет являться нормализованной суммой векторов Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_2} , если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha_{12}<\frac{\pi}{2}} и противоположен этой сумме, если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha_{12}>\frac{\pi}{2}} .

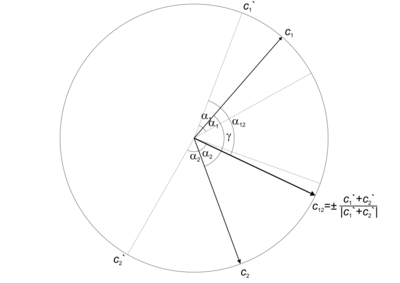
Существует три случая.

Объединение секторов, у которых Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1\|\vec{c}_2} .

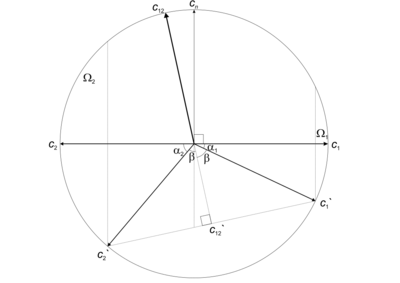
Рассмотрим случай, когда Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1\|\vec{c}_2} . Поскольку длины всех векторов равны единице, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_2=-\vec{c}_1} , а количество плоскостей, которым одновременно могут принадлежать Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_2} бесконечно, вследствие чего количество возможных секторов минимальной площади, объединяющих Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Omega_1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Omega_2} , также бесконечно и зависит от того на какой из плоскостей будут принадлежать выбранные Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_2} ; и этот выбор будет сводится к выбору диаметральной плоскости, проходящей через Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1} .

Этот выбор можно сделать, если задать произвольный вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_n} , перпендикулярный Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1} .

В описываемой реализации

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_n=\left[\begin{matrix} \begin{pmatrix}1 & 0 & 0\end{pmatrix}^T,\Leftrightarrow \vec{c}_1.x\equiv 0 \\ \begin{pmatrix}-\frac{\vec{c}_1.y}{\vec{c}_1.x} & 1 & 0\end{pmatrix}^T,\Leftrightarrow \vec{c}_1.x\equiv 0 \end{matrix}\right.} .

Тогда на плоскости, которой одновременно принадлежат Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1} , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_2} , будет однозначно определен вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_{12}} , отстоящий на одинаковом угловом расстоянии от векторов Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_1} и ${\vec {c'}}_{2}$ и, поэтому, параллельный вектору Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_{12}} центральной точки сектора-объединения.

Для нахождения вектора Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_{12}} достаточно выразить его в базисе Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\langle\vec{c}_1,\vec{c}_n\right\rangle} и осуществить переход к мировой системе координат входной модели. Как видно из рисунка, в указанном базисе вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_{12}} имеет координаты

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{pmatrix} \left|\vec{c}_1\right|\cdot\textrm{cos}\left(\frac{\pi}{2} - \beta\right)\textrm{cos}\left(\frac{\pi}{2}-\left(\alpha_1 + \beta\right)\right) \\ \left|\vec{c}_1\right|\cdot\textrm{cos}\left(\frac{\pi}{2} - \beta\right)\textrm{sin}\left(\frac{\pi}{2}-\left(\alpha_1 + \beta\right)\right) \end{pmatrix} = \begin{pmatrix} \textrm{cos}\left(\frac{\pi}{2} - \beta\right)\textrm{cos}\left(\frac{\pi}{2}-\left(\alpha_1 + \beta\right)\right) \\ \textrm{cos}\left(\frac{\pi}{2} - \beta\right)\textrm{sin}\left(\frac{\pi}{2}-\left(\alpha_1 + \beta\right)\right) \end{pmatrix}} ,

причем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \beta=\frac{\pi-\left(\alpha_1 + \alpha_2\right)}{2}=\frac{\pi}{2}-\frac{\alpha_1 + \alpha_2}{2}} .

Тогда в мировых координатах

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c'}_{12}=\begin{pmatrix}\vec{c}_1 & \vec{c}_n\end{pmatrix} \begin{pmatrix} \textrm{cos}\left(\frac{\pi}{2} - \frac{\alpha_1 + \alpha_2}{2}\right)\textrm{cos}\left(\frac{\pi}{2}+\frac{\alpha_1 - \alpha_2}{2}\right) \\ \textrm{cos}\left(\frac{\pi}{2} - \frac{\alpha_1 + \alpha_2}{2}\right)\textrm{sin}\left(\frac{\pi}{2}+\frac{\alpha_1 - \alpha_2}{2}\right) \end{pmatrix}} .

Тогда Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_{12} = -\frac{\vec{c'}_{12}}{\left|\vec{c'}_{12}\right|}} , а Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha_{12}=\pi - \beta = \frac{\pi}{2}+\frac{\alpha_1 + \alpha_2}{2}} .

Во втором случае Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1\nparallel\vec\vec{c}_2} , однако Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c}_1\|\vec{c}_2} .