Распространение радиоволн ВЧ/Реализация/radiation set t: различия между версиями
(Исправлены ошибки в коде программы и документации) |
|||
| Строка 23: | Строка 23: | ||
Функция <math>\delta\left(S, \theta, \varphi\right)</math> преобразования ангулярных координат относительно <math>\vec{c_p}</math> источника <math>S</math> к базису <math>S</math> реализуется поворотом вектора <math>\vec{c_p}</math> так, чтобы он совпал с направлением главной оси источника (которая в свою очередь совпадает с аппликатой базиса источника). То есть используется матрица поворота | Функция <math>\delta\left(S, \theta, \varphi\right)</math> преобразования ангулярных координат относительно <math>\vec{c_p}</math> источника <math>S</math> к базису <math>S</math> реализуется поворотом вектора <math>\vec{c_p}</math> так, чтобы он совпал с направлением главной оси источника (которая в свою очередь совпадает с аппликатой базиса источника). То есть используется матрица поворота | ||
:<math>T\left(\vec{c_p}\right)=\begin{bmatrix} | :<math>T\left(\vec{c_p}\right)=\begin{bmatrix} | ||
\textrm{cos}\varphi_{cp} & 0 & \textrm{sin}\varphi_{cp} \\ | \textrm{cos}\varphi_{cp} & 0 & -\textrm{sin}\varphi_{cp} \\ | ||
0 & 1 & 0 \\ | 0 & 1 & 0 \\ | ||
\textrm{sin}\varphi_{cp} & 0 & \textrm{cos}\varphi_{cp} | |||
\end{bmatrix}\begin{bmatrix} | \end{bmatrix}\begin{bmatrix} | ||
\textrm{cos}\theta_{cp} & | \textrm{cos}\theta_{cp} & \textrm{sin}\theta_{cp} & 0 \\ | ||
\textrm{sin}\theta_{cp} & \textrm{cos}\theta_{cp} & 0 \\ | -\textrm{sin}\theta_{cp} & \textrm{cos}\theta_{cp} & 0 \\ | ||
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{bmatrix}= | |||
\begin{bmatrix} | |||
\textrm{cos}\theta_{cp}\textrm{cos}\varphi_{cp} & \textrm{sin}\theta_{cp}\textrm{cos}\varphi_{cp} & -\textrm{sin}\varphi_{cp} \\ | |||
-\textrm{sin}\theta_{cp} & \textrm{cos}\theta_{cp} & 0 \\ | |||
\textrm{cos}\theta_{cp}\textrm{sin}\varphi_{cp} & \textrm{sin}\theta_{cp}\textrm{sin}\varphi_{cp} & \textrm{cos}\varphi_{cp} | |||
\end{bmatrix}</math>, | \end{bmatrix}</math>, | ||
в которой пара значений <math>\begin{pmatrix}\theta_{cp} & \varphi_{cp}\end{pmatrix}</math> возвращается вызванным над <math>\vec{c_p}</math> методом [[Распространение радиоволн ВЧ/Реализация/Antenna::ToSpherical|Antenna::ToSpherical]] антенны источника <math>S</math> (см. [[Распространение радиоволн ВЧ/Реализация/Source::Antenna|Source::Antenna]]). | в которой пара значений <math>\begin{pmatrix}\theta_{cp} & \varphi_{cp}\end{pmatrix}</math> возвращается вызванным над <math>\vec{c_p}</math> методом [[Распространение радиоволн ВЧ/Реализация/Antenna::ToSpherical|Antenna::ToSpherical]] антенны источника <math>S</math> (см. [[Распространение радиоволн ВЧ/Реализация/Source::Antenna|Source::Antenna]]). | ||
Тогда направление, заданное углами <math>\left(\theta,\varphi\right)</math> относительно <math>\vec{c_p}</math>, в базисе источника будет иметь представление | Тогда направление, заданное углами <math>\left(\theta,\varphi\right)</math> относительно <math>\vec{c_p}</math>, в базисе источника будет иметь представление | ||
:<math>P\left(\vec{c_p}, \theta,\varphi\right)=T\left(\vec{c_p}\right)\begin{bmatrix} | :<math>P\left(\vec{c_p}, \theta,\varphi\right)=\left(T\left(\vec{c_p}\right)\right)^{-1}\begin{bmatrix} | ||
\textrm{sin}\varphi\textrm{cos}\theta \\ | |||
\textrm{sin}\varphi\textrm{sin}\theta \\ | |||
\textrm{cos}\varphi | |||
\end{bmatrix} = \left(T\left(\vec{c_p}\right)\right)^T \begin{bmatrix} | |||
\textrm{sin}\varphi\textrm{cos}\theta \\ | |||
\textrm{sin}\varphi\textrm{sin}\theta \\ | |||
\textrm{cos}\varphi | |||
\end{bmatrix} = | |||
\begin{bmatrix} | |||
\textrm{cos}\theta_{cp}\textrm{cos}\varphi_{cp} & -\textrm{sin}\theta_{cp} & \textrm{cos}\theta_{cp}\textrm{sin}\varphi_{cp} \\ | |||
\textrm{sin}\theta_{cp}\textrm{cos}\varphi_{cp} & \textrm{cos}\theta_{cp} & \textrm{sin}\theta_{cp}\textrm{sin}\varphi_{cp} \\ | |||
-\textrm{sin}\varphi_{cp} & 0 & \textrm{cos}\varphi_{cp} | |||
\end{bmatrix} \cdot | |||
\begin{bmatrix} | |||
\textrm{sin}\varphi\textrm{cos}\theta \\ | \textrm{sin}\varphi\textrm{cos}\theta \\ | ||
\textrm{sin}\varphi\textrm{sin}\theta \\ | \textrm{sin}\varphi\textrm{sin}\theta \\ | ||
| Строка 44: | Строка 63: | ||
\left[ | \left[ | ||
\begin{matrix} | \begin{matrix} | ||
\begin{pmatrix}0 & | \begin{pmatrix}0 & 0\end{pmatrix} \Leftrightarrow P_x^2 + P_y^2 \equiv 0 \\ | ||
\begin{pmatrix}\textrm{sign}\left(P_y\right)\cdot\textrm{acos}\frac{P_x}{P_x^2+P_y^2} & \textrm{acos}\frac{P_z}{\left|P\right|}\end{pmatrix} \Leftrightarrow P_x^2 + P_y^2 \ne 0 \\ | \begin{pmatrix}\textrm{sign}\left(P_y\right)\cdot\textrm{acos}\frac{P_x}{P_x^2+P_y^2} & \textrm{acos}\frac{P_z}{\left|P\right|}\end{pmatrix} \Leftrightarrow P_x^2 + P_y^2 \ne 0 \\ | ||
\end{matrix} | \end{matrix} | ||
Текущая версия на 19:37, 8 декабря 2020
Реализует перечисление направлений излучения источником элементов волнового поля при использовании итерационного алгоритма рей-трейсинга.
template <class RadiationPatternType>
using radiation_set_t = dyn_radiation_set_dim_1_collection<RadiationPatternType>;
| RadiationPatternType | Тип характеристики направленности, для которой осуществляется перечисление. |
Тип реализует двумерную коллекцию направлений излучения, которая создается для заданного источника поля и зависит от частоты излучения, номера итерации, а также от позиций отражающих поверхностей и контрольных точек относительно источника.
Измерения индексируются с нуля. Первое, внешнее, измерение реализуется классами dyn_radiation_set_dim_1_collection и dyn_radiation_set_dim_1_enumerator, первый из которых реализует коллекцию направлений в этом измерении, а второй - перечисление коллекций нулевого измерения для каждого элемента коллекции в первом измерении.
Нулевое измерение реализуется классами dyn_radiation_set_dim_0_collection и dyn_radiation_set_dim_0_enumerator соответственно. Элементами коллекции в нулевом измерении являются пары угловых значений "азимут-зенит", реализуемые структурой angle_pair.
Реализация перечисленных классов определяет в нулевом измерении перечисление азимутов Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta и в первом измерении - зенитов Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi .
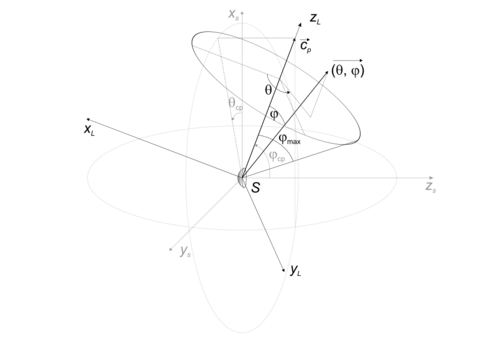
При формировании коллекции направлений излучения производится минимизация числа элементов коллекции двумя способами. Первый - это зависимость ангулярного шага от значения функции характеристики направленности в текущей ангулярной позиции, как это описано для итерационного рей-трейсинга. Второй способ представляет собой ограничение сферы вокруг источника так, чтобы полученный сектор охватывал все отражающие поверхности и контрольные точки входной геометрической модели, и исключение из множества направлений тех из них, которые не принадлежат этому сектору. См. описание класса encompassing_aperture_t, который описывает такой сектор с помощью вектора направления на центральную точку сектора и ангулярного радиуса вокруг этого вектора.
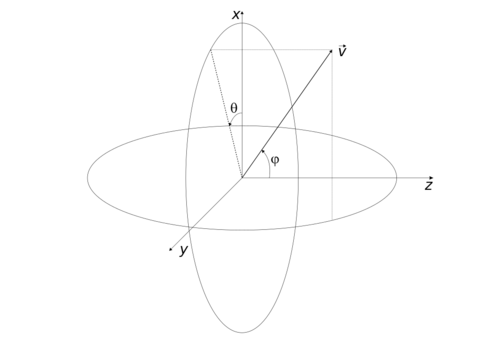
Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta_{0, \textrm{min}}} - управляющее значение, возвращенное методом Config::AngularSamplingRateMin, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta_{0, \textrm{max}}} - управляющее значение, возвращенное методом Config::AngularSamplingRateMax, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle R\left(\omega,\theta,\varphi\right)} - функция характеристики направленности источника, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i\ge 0} - номер текущей итерации, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \delta\left(S, \theta, \varphi\right)} - функция перехода от азимута Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta и зенита Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi , выраженных относительно вектора Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c_p}} источника (см. рисунок), к азимуту и зениту, выраженным относительно главной оси источника, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{pmatrix}\theta_s & \varphi_s \end{pmatrix} = \delta\left(S, \theta, \varphi\right)} . Тогда ангулярный шаг в нулевом измерении расчитывается как функция
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta_\theta\left(\omega,\theta,\varphi\right) = \frac{\Delta_{0, \textrm{min}} + \left(\Delta_{0, \textrm{max}} - \Delta_{0, \textrm{min}}\right)\left(1 - R\left(\omega,\theta_s,\varphi_s\right)\right)}{2^i}} .
Зенит перечисляется в первом измерении с шагом Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta_\varphi\left(\omega,\varphi\right)=\Delta_\theta\left(\omega,0,\varphi\right)} .
Функция Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \delta\left(S, \theta, \varphi\right)} преобразования ангулярных координат относительно Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c_p}} источника Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S к базису Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S реализуется поворотом вектора Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c_p}} так, чтобы он совпал с направлением главной оси источника (которая в свою очередь совпадает с аппликатой базиса источника). То есть используется матрица поворота
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T\left(\vec{c_p}\right)=\begin{bmatrix} \textrm{cos}\varphi_{cp} & 0 & -\textrm{sin}\varphi_{cp} \\ 0 & 1 & 0 \\ \textrm{sin}\varphi_{cp} & 0 & \textrm{cos}\varphi_{cp} \end{bmatrix}\begin{bmatrix} \textrm{cos}\theta_{cp} & \textrm{sin}\theta_{cp} & 0 \\ -\textrm{sin}\theta_{cp} & \textrm{cos}\theta_{cp} & 0 \\ 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} \textrm{cos}\theta_{cp}\textrm{cos}\varphi_{cp} & \textrm{sin}\theta_{cp}\textrm{cos}\varphi_{cp} & -\textrm{sin}\varphi_{cp} \\ -\textrm{sin}\theta_{cp} & \textrm{cos}\theta_{cp} & 0 \\ \textrm{cos}\theta_{cp}\textrm{sin}\varphi_{cp} & \textrm{sin}\theta_{cp}\textrm{sin}\varphi_{cp} & \textrm{cos}\varphi_{cp} \end{bmatrix}} ,
в которой пара значений Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{pmatrix}\theta_{cp} & \varphi_{cp}\end{pmatrix}} возвращается вызванным над Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c_p}} методом Antenna::ToSpherical антенны источника Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S (см. Source::Antenna).
Тогда направление, заданное углами Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left(\theta,\varphi\right)} относительно Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\vec {c_{p}}}} , в базисе источника будет иметь представление
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P\left(\vec{c_p}, \theta,\varphi\right)=\left(T\left(\vec{c_p}\right)\right)^{-1}\begin{bmatrix} \textrm{sin}\varphi\textrm{cos}\theta \\ \textrm{sin}\varphi\textrm{sin}\theta \\ \textrm{cos}\varphi \end{bmatrix} = \left(T\left(\vec{c_p}\right)\right)^T \begin{bmatrix} \textrm{sin}\varphi\textrm{cos}\theta \\ \textrm{sin}\varphi\textrm{sin}\theta \\ \textrm{cos}\varphi \end{bmatrix} = \begin{bmatrix} \textrm{cos}\theta_{cp}\textrm{cos}\varphi_{cp} & -\textrm{sin}\theta_{cp} & \textrm{cos}\theta_{cp}\textrm{sin}\varphi_{cp} \\ \textrm{sin}\theta_{cp}\textrm{cos}\varphi_{cp} & \textrm{cos}\theta_{cp} & \textrm{sin}\theta_{cp}\textrm{sin}\varphi_{cp} \\ -\textrm{sin}\varphi_{cp} & 0 & \textrm{cos}\varphi_{cp} \end{bmatrix} \cdot \begin{bmatrix} \textrm{sin}\varphi\textrm{cos}\theta \\ \textrm{sin}\varphi\textrm{sin}\theta \\ \textrm{cos}\varphi \end{bmatrix}}
Поэтому результирующая пара углов вычисляется следующим образом
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{pmatrix}\theta_s & \varphi_s\end{pmatrix} = \left[ \begin{matrix} \begin{pmatrix}0 & 0\end{pmatrix} \Leftrightarrow P_x^2 + P_y^2 \equiv 0 \\ \begin{pmatrix}\textrm{sign}\left(P_y\right)\cdot\textrm{acos}\frac{P_x}{P_x^2+P_y^2} & \textrm{acos}\frac{P_z}{\left|P\right|}\end{pmatrix} \Leftrightarrow P_x^2 + P_y^2 \ne 0 \\ \end{matrix} \right.}
Область определения функции Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \delta\left(S, \theta, \varphi\right)} : Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta\in\left[0, 2\pi\right)} , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varphi\in\left[0, \varphi_{\textrm{max}}\right]\subset\left[0, \pi\right]} , где Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varphi_{\textrm{max}}} - максимально возможный зенит - ангулярный радиус, значение которого возвращается методом encompassing_aperture_t::radius, сектора сферы вокруг источника, так что все отражающие объекты и контрольные точки геометрической модели при отображении на сферу оказываются внутри сектора. При этом вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{c_p}} , возвращаемый методом encompassing_aperture_t::central_point, направлен на центр такого сектора.
 (азимута) относительно некоторого центрального направления Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}}
. В случае отсутствия оптимизации по локальности отражающих поверхностей и контрольных точек Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}}
совпадает с главной осью источника. Если же используется оптимизация, вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}}
совпадает с вектором, возвращаемым методом
(азимута) относительно некоторого центрального направления Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}}
. В случае отсутствия оптимизации по локальности отражающих поверхностей и контрольных точек Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}}
совпадает с главной осью источника. Если же используется оптимизация, вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}}
совпадает с вектором, возвращаемым методом  (см. рисунок), к азимуту и зениту, выраженным относительно главной оси источника, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{pmatrix}\theta_s & \varphi_s \end{pmatrix} = \delta\left(S, \theta, \varphi\right)}
. Тогда ангулярный шаг в нулевом измерении расчитывается как функция
(см. рисунок), к азимуту и зениту, выраженным относительно главной оси источника, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{pmatrix}\theta_s & \varphi_s \end{pmatrix} = \delta\left(S, \theta, \varphi\right)}
. Тогда ангулярный шаг в нулевом измерении расчитывается как функция