Шаблон:Распространение радиоволн ВЧ/Реализация/EncompassingAperture/Алгоритм: различия между версиями
(Новая страница: «Пусть <math>V=\begin{pmatrix}\vec{v}_0, \cdots, \vec{v}_{n-1}\end{pmatrix}</math> - непустое входное множество геометричес…») |
|||
| Строка 4: | Строка 4: | ||
Фактически, это означает, что все углы, образованные всеми возможными парами отрезков от <math>P</math> до <math>\forall\vec{v}_i\in V</math> должны быть меньше <math>\pi</math>. Это имеет место, когда <math>V</math> образовано, например, вершинами одной отражающей поверхности [[Распространение радиоволн ВЧ/Реализация/ReflectingObject|ReflectingObject]] или контрольными точками одной плоскости вывода результатов [[Распространение радиоволн ВЧ/Реализация/PlainControlPointSet|PlainControlPointSet]]. См. также [[Распространение радиоволн ВЧ/Реализация/Source::OptimizeRadiationVectors|Source::OptimizeRadiationVectors]]. | Фактически, это означает, что все углы, образованные всеми возможными парами отрезков от <math>P</math> до <math>\forall\vec{v}_i\in V</math> должны быть меньше <math>\pi</math>. Это имеет место, когда <math>V</math> образовано, например, вершинами одной отражающей поверхности [[Распространение радиоволн ВЧ/Реализация/ReflectingObject|ReflectingObject]] или контрольными точками одной плоскости вывода результатов [[Распространение радиоволн ВЧ/Реализация/PlainControlPointSet|PlainControlPointSet]]. См. также [[Распространение радиоволн ВЧ/Реализация/Source::OptimizeRadiationVectors|Source::OptimizeRadiationVectors]]. | ||
[[Файл:EncompassingAperture-algo bisector triangle.svg|thumb|Поиск центральной точки сферы и ангулярного радиуса при конструировании объекта [[Распространение радиоволн ВЧ/Реализация/encompassing_aperture_t|encompassing_aperture_t]] на основе позиции точки <math>\vec{P}</math>, вокруг которой строится сфера, и двух точек, которые ограничивают площадь сектора. Вектора <math>\vec{v}_1</math> и <math>\vec{v}_2</math> на рисунке соответствуют векторам <math>\vec{v'}_i</math> и <math>\vec{v'}_j</math> в статье.|500px]] | |||
Если <math>\left|V\right|\equiv 1</math>, то <math>\Omega=\left\langle\frac{\vec{v}_0-\vec{P}}{\left|\vec{v}_0-\vec{P}\right|}, 0\right\rangle</math>. Далее по тексту <math>\left|V\right|\ge 2</math>. | Если <math>\left|V\right|\equiv 1</math>, то <math>\Omega=\left\langle\frac{\vec{v}_0-\vec{P}}{\left|\vec{v}_0-\vec{P}\right|}, 0\right\rangle</math>. Далее по тексту <math>\left|V\right|\ge 2</math>. | ||
Текущая версия на 01:50, 3 декабря 2018
Пусть - непустое входное множество геометрических точек, и - некоторая заданная точка, вокруг которой требуется построить сектор сферы с единичным радиусом, где - вектор, ассоциированный с направленным отрезком от до центральной точки сектора на поверхности сферы, и - ангулярный радиус сектора, как это реализуется классом encompassing_aperture_t. Проекции всех точек из на сферу должны принадлежать .
Пусть также все точки из лежат по одну сторону от , т.е. не находится геометрически в облаке, образованном . Если это не так, то множество должно быть разбито на подмножества точек, лежащих по одну сторону от , а затем сектора, образованные применением описываемого алгоритма над и подмножествами, должны быть объединены с помощью функции unify.
Фактически, это означает, что все углы, образованные всеми возможными парами отрезков от до должны быть меньше . Это имеет место, когда образовано, например, вершинами одной отражающей поверхности ReflectingObject или контрольными точками одной плоскости вывода результатов PlainControlPointSet. См. также Source::OptimizeRadiationVectors.

Если , то . Далее по тексту .
Создадим множество и выберем пару тех точек, отрезки из до которых образуют между собой наибольший угол .
Если угол равен нулю, то .
Поэтому далее по тексту рассматривается оставшийся случай, когда , и .
Тогда задача нахождения будет сводиться к нахождению биссектрисы между и , лежащий на ней вектор единичной длины и угол .
Для нахождения вектора соединим прямой точки и и обозначим как вектор, с которым ассоциирован направленный отрезок, имеющий начало в точке , направленный вдоль биссектриссы между и до точки пересечения с прямой. Обозначим как вектор, с которым ассоциирован направленный отрезок с началом в конце отрезка и концом в точке пересечения. То есть
- .
Согласно теореме о биссектрисе эта точка делит отрезок между и в пропорции, равной отношению длин и . Поэтому
- ;
- .
Поэтому
- .
Пусть и
- .
Тогда и .
 - непустое входное множество геометрических точек, и
- непустое входное множество геометрических точек, и 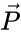 - некоторая заданная точка, вокруг которой требуется построить сектор
- некоторая заданная точка, вокруг которой требуется построить сектор  сферы с единичным радиусом, где
сферы с единичным радиусом, где 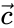 - вектор, ассоциированный с направленным отрезком от
- вектор, ассоциированный с направленным отрезком от  - ангулярный радиус сектора, как это реализуется классом
- ангулярный радиус сектора, как это реализуется классом 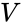 на сферу должны принадлежать
на сферу должны принадлежать 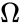 .
.
 , т.е.
, т.е.  должны быть меньше
должны быть меньше  . Это имеет место, когда
. Это имеет место, когда  и
и  на рисунке соответствуют векторам
на рисунке соответствуют векторам  и
и  в статье.
в статье. , то
, то  . Далее по тексту
. Далее по тексту  .
.
 и выберем пару
и выберем пару  тех точек, отрезки из
тех точек, отрезки из 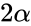 .
.
 .
.
 и
и  .
.
 .
.
 вектор, с которым ассоциирован направленный отрезок, имеющий начало в точке
вектор, с которым ассоциирован направленный отрезок, имеющий начало в точке  вектор, с которым ассоциирован направленный отрезок с началом в конце отрезка
вектор, с которым ассоциирован направленный отрезок с началом в конце отрезка  .
. и
и  . Поэтому
. Поэтому
 ;
; .
. .
. и
и
 .
. и
и