Распространение радиоволн ВЧ/Напряженность: различия между версиями
| Строка 8: | Строка 8: | ||
В результате распространения излученного элемента волны на расстояние <math>r_1</math> напряженность поля падает в <math>r_1 e^{ikr_1}</math> раз, становясь равной | В результате распространения излученного элемента волны на расстояние <math>r_1</math> напряженность поля падает в <math>r_1 e^{ikr_1}</math> раз, становясь равной | ||
:<math>\vec{\dot E}\left(r_1\right)=\vec{\dot E_0}r_0 y_1 = \vec{\dot E_0}\frac{r_0}{r_1}e^{-ikr_1}</math>, где: | :<math>\vec{\dot E}\left(r_1\right)=\vec{\dot E_0}r_0 y_1 \left(r_1\right) = \vec{\dot E_0}\frac{r_0}{r_1}e^{-ikr_1}</math>, где: | ||
* <math>y_1 | * <math>y_1 \left(r_1\right) = \frac{1}{r_1}e^{-ikr_1}</math> - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны, | ||
* <math>\dot k = \omega \sqrt{\dot \varepsilon \dot \mu}</math> - комплексное волновое число | * <math>\dot k = \omega \sqrt{\dot \varepsilon \dot \mu}</math> - комплексное волновое число | ||
** <math>\dot \varepsilon = \varepsilon' - i \varepsilon''</math> | ** <math>\dot \varepsilon = \varepsilon' - i \varepsilon''</math> | ||
| Строка 26: | Строка 26: | ||
Тогда, в результате распространения волнового элемента на расстояние <math>r_1 + r_2</math> от источника в одной и той же изотропной среде, результирующая напряженность станет равной | Тогда, в результате распространения волнового элемента на расстояние <math>r_1 + r_2</math> от источника в одной и той же изотропной среде, результирующая напряженность станет равной | ||
:<math>\vec{\dot E}\left(r_1 | :<math>\vec{\dot E}\left(r_1, r_2\right) = \vec{\dot E_0}r_0 y\left(r_1, r_2\right)=\vec{\dot E_0}r_0 y_1\left(r_1, r_2\right)\left(r_1, r_2\right)y_2\left(r_1, r_2\right)</math>, | ||
где <math> | где <math>y_1\left(r_1, r_2\right) = \left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{1}{2}}\frac{e^{-ikr_1}}{r_1}</math>, <math>y'_2\left(r_1, r_2\right) = \left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{1}{2}}\frac{e^{-ikr_2}}{r_2}</math> и <math>y\left(r_1, r_2\right) = y_1\left(r_1, r_2\right)y_2\left(r_1, r_2\right)=\left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{2}{2}}\frac{e^{-ikr_1}e^{-ikr_2}}{r_1 r_2} = \frac{e^{-ik\left(r_1 + r_2\right)}}{r_1 + r_2}</math>. | ||
В более общем случае | |||
:<math>\vec{\dot E}\left(r_1, \dots, r_n\right) = \vec{\dot E_0}r_0 y\left(r_1, \dots, r_n\right)=\vec{\dot E_0}r_0\prod_{j=1}^{n}y_j\left(r_1, \dots, r_n\right)= | |||
:<math>\vec{\dot E}\left(\ | \vec{\dot E_0}\frac{r_0}{\sum_{i=1}^{n} r_i}e^{-i\left(\sum_{i=1}^{n} k_i r_i\right)}</math>, | ||
где <math>y_j\left(r_1, \dots, r_n\right) = \left(\frac{\prod_{j'=1}^{n}r_{j'}}{\sum_{j'=1}^{n}r_{j'}}\right)^\frac{1}{n}\frac{e^{-ik_jr_j}}{r_j}</math>. | |||
=Модель отражения= | =Модель отражения= | ||
Версия 19:50, 23 сентября 2018
Трехкомпонентный комплексный вектор который задается волновым элементом, порождаемым источником , в результате распространения и отражений в среде.
Вектор рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
Модель распространения
Пусть - дальняя зона, расстояние, на котором для источника снята начальная напряженность .
В результате распространения излученного элемента волны на расстояние напряженность поля падает в раз, становясь равной
- , где:
- - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны,
- - комплексное волновое число
Таким образом .
Здесь первая экспонента является коэффициентом поглощения среды на расстоянии , а
- погонным затуханием среды [дБ/м]
В частности, при отсутствии инерционности поляризации и намагничивания :
.
Тогда, в результате распространения волнового элемента на расстояние от источника в одной и той же изотропной среде, результирующая напряженность станет равной
- ,
где , и .
В более общем случае
- ,
где .
Модель отражения
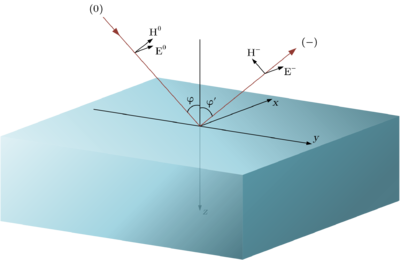
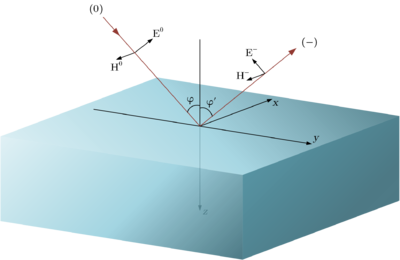
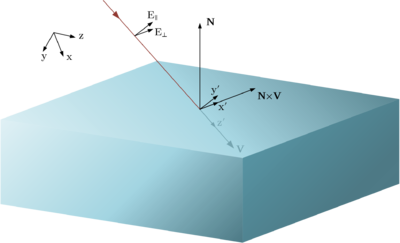
Пусть электрическая напряженность волнового элемента, падающего на плоскую поверхность с нормалью , задается некоторым комплексным вектором . Пусть эта поверхность является границей раздела двух сред: - среды, в которой распространяется падающая волна, задаваемой четверкой параметров и - среды, на границу которой падает волна, задаваемой четверкой параметров .
Здесь:
- - комплексная диэлектрическая проницаемость, где
- - диэлектрическая проницаемость среды,
- - проводимость среды,
- - круговая частота волны,
- - угол диэлектрических потерь;
- - комплексная магнитная проницаемость, где
- - магнитная проницаемость среды,
- - угол магнитных потерь;
- - комплексное волновое число;
- - комплексное волновое сопротивление.
Тогда коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля):
,
, где - угол падения.
Таким образом отраженная волна имеет вид
Функции
Изменить по пробегу(Напряженность, Пробег, Комплексное волновое число)
При распространении радиоволны в свободном пространстве происходит изменение ее фазы и амплитуды. Амплитуда уменьшается вследствии сферической расходимости волны, а также при распространении в поглощающих средах - вследствии поглощения в среде.
, где
- - напряженность в начальной точке
- - пройденное расстояние
- - комплексное волновое число
Как видно из формулы первая экспонента является коэффициентом поглощения среды на расстоянии r, а
- погонным затуханием среды [дБ/м]
В частности, при отсутствии инерционности поляризации и намагничивания :
На вход функции принимается трехкомпонентный комплексный вектор напряженности, расстояние пробега волны и комплексное волновое число. На выходе получаем трехкомпонентный комплексный вектор напряженности, прошедший заданное расстояние.
- Напряженность
- Пробег
- Комплексное волновое число
Изменить по отражению(Напряженность, КДП_1*, КМП_1**, КДП_2, КМП_2, Угол, Вектор(Направление луча), Вектор(Нормаль грани))
* - комплексная диэлектрическая проницаемость, ** - комплексная магнитная проницаемость.
Пусть имеется граница раздела двух сред:
- комплексная диэлектрическая проницаемость, где
- - диэлектрическая проницаемость среды,
- - проводимость среды
- - круговая частота волны
- магнитная проницаемость
При учете инерционности поляризации и намагничивания вводятся следующие комплексные проницаемости:
, где
- - угол диэлектрических потерь
- - угол магнитных потерь
- комплексное волновое число
- комплексное волновое сопротивление
Коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля):
, где
- - угол падения
Таким образом отраженная волна имеет вид
Т.к. напряженность поля дана в виде трехкомпонентного вектора относительно глобальной системы координат, необходимо найти параллельную и перпендикулярную составляющие соответственно данной грани и падающему лучу. Для этого составим матрицы поворота координатных осей таким образом, чтобы ось z совпала с направляющим вектором луча, а ось x с вектором векторного произведения направляющего вектора луча и вектора нормали грани. В результате в новых координатах .
На вход функции подается трехкомпонентный комплексный вектор напряженности, комплексные диэлектрические и магнитные проницаемости обоих сред, причем первыми даются характеристики среды из которой пришел луч. Также на вход функции поступает угол падения, направляющий вектор луча и вектор нормали грани. На выходе получаем трехкомпонентный вектор отраженной напряженности в глобальных координатах.
- Вектор(Направление луча)
- Вектор(Нормаль грани)
- Напряженность
- Угол
- КДП_1
- КДП_2
- КМП_1
- КМП_2
 который задается волновым элементом, порождаемым
который задается волновым элементом, порождаемым  , в результате распространения и отражений в среде.
, в результате распространения и отражений в среде.
 рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
 - дальняя зона, расстояние, на котором для источника
- дальняя зона, расстояние, на котором для источника  .
.
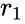 напряженность поля падает в
напряженность поля падает в  раз, становясь равной
раз, становясь равной
 , где:
, где: - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны,
- скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны, - комплексное волновое число
- комплексное волновое число



 .
.
 - погонным затуханием среды [дБ/м]
- погонным затуханием среды [дБ/м]
 :
:
 .
.
 от источника в одной и той же изотропной среде, результирующая напряженность станет равной
от источника в одной и той же изотропной среде, результирующая напряженность станет равной
 ,
, ,
,  и
и  .
.
 ,
, .
.
 , задается некоторым комплексным вектором
, задается некоторым комплексным вектором  . Пусть эта поверхность является границей раздела двух сред:
- среды, в которой распространяется падающая волна, задаваемой четверкой параметров
. Пусть эта поверхность является границей раздела двух сред:
- среды, в которой распространяется падающая волна, задаваемой четверкой параметров  и
- среды, на границу которой падает волна, задаваемой четверкой параметров
и
- среды, на границу которой падает волна, задаваемой четверкой параметров  .
.
 - комплексная диэлектрическая проницаемость, где
- комплексная диэлектрическая проницаемость, где
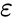 - диэлектрическая проницаемость среды,
- диэлектрическая проницаемость среды, - проводимость среды,
- проводимость среды, - круговая частота волны,
- круговая частота волны, - угол диэлектрических потерь;
- угол диэлектрических потерь; - комплексная магнитная проницаемость, где
- комплексная магнитная проницаемость, где
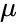 - магнитная проницаемость среды,
- магнитная проницаемость среды, - угол магнитных потерь;
- угол магнитных потерь; - комплексное волновое сопротивление.
- комплексное волновое сопротивление. ,
,
 ,
где
,
где  - угол падения.
- угол падения.

 , где
, где
 - напряженность в начальной точке
- напряженность в начальной точке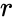 - пройденное расстояние
- пройденное расстояние
 Напряженность
Напряженность Пробег
Пробег Комплексное волновое число
Комплексное волновое число


 - комплексная диэлектрическая проницаемость, где
- комплексная диэлектрическая проницаемость, где

 .
.
 Вектор(Направление луча)
Вектор(Направление луча) Вектор(Нормаль грани)
Вектор(Нормаль грани) Угол
Угол КДП_1
КДП_1 КДП_2
КДП_2 КМП_1
КМП_1 КМП_2
КМП_2




