Распространение радиоволн ВЧ/Напряженность: различия между версиями
Nigiluk (обсуждение | вклад) |
Nigiluk (обсуждение | вклад) |
||
| Строка 45: | Строка 45: | ||
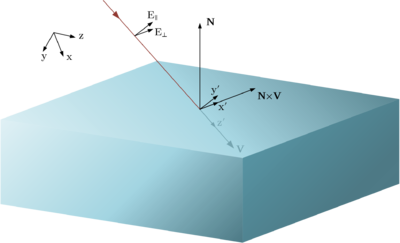
Т.к. напряженность поля дана в виде трехкомпонентного вектора относительно глобальной системы координат, необходимо найти параллельную и перпендикулярную составляющие соответственно данной грани и падающему лучу. Для этого составим матрицы поворота координатных осей таким образом, чтобы ось z совпала с направляющим вектором луча, а ось x с вектором векторного произведения направляющего вектора луча и вектора нормали грани. В результате в новых координатах <math>E_x=E_{\bot},~E_y=E_{\|},~E_z=0</math>. | Т.к. напряженность поля дана в виде трехкомпонентного вектора относительно глобальной системы координат, необходимо найти параллельную и перпендикулярную составляющие соответственно данной грани и падающему лучу. Для этого составим матрицы поворота координатных осей таким образом, чтобы ось z совпала с направляющим вектором луча, а ось x с вектором векторного произведения направляющего вектора луча и вектора нормали грани. В результате в новых координатах <math>E_x=E_{\bot},~E_y=E_{\|},~E_z=0</math>. | ||
На вход функции подается трехкомпонентный комплексный вектор напряженности, комплексные диэлектрические и магнитные проницаемости обоих сред, причем первыми даются характеристики среды из которой пришел луч. Также на вход функции поступает угол падения, направляющий вектор луча и вектор нормали грани. | На вход функции подается трехкомпонентный комплексный вектор напряженности, комплексные диэлектрические и магнитные проницаемости обоих сред, причем первыми даются характеристики среды из которой пришел луч. Также на вход функции поступает угол падения, направляющий вектор луча и вектор нормали грани. На выходе получаем трехкомпонентный вектор отраженной напряженности в глобальных координатах. | ||
#<math>V\leftarrow</math> <tt>Вектор(Направление луча)</tt> | #<math>V\leftarrow</math> <tt>Вектор(Направление луча)</tt> | ||
| Строка 55: | Строка 55: | ||
#<math>\mu_1 \leftarrow</math> <tt>КМП_1</tt> | #<math>\mu_1 \leftarrow</math> <tt>КМП_1</tt> | ||
#<math>\mu_2 \leftarrow</math> <tt>КМП_2</tt> | #<math>\mu_2 \leftarrow</math> <tt>КМП_2</tt> | ||
#<math>K \leftarrow N \times V</math> | #<math>K \leftarrow N \times V</math> | ||
#<math> | #<math>E \leftarrow \begin{bmatrix} E(1) & E(2) & E(3) \end{bmatrix} \begin{bmatrix} \frac {V(3)} {\sqrt {V(1)^2+V(3)^2}} & 0 & \frac {V(1)} {\sqrt {V(1)^2+V(3)^2}} \\ 0 & 1 & 0 \\ -\frac {V(1)} {\sqrt {V(1)^2+V(3)^2}} & 0 & \frac {V(3)} {\sqrt {V(1)^2+V(3)^2}} \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac {\sqrt {V(1)^2+V(3)^2}} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} & \frac {V(2)} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} \\ 0 & -\frac {V(2)} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} & \frac {\sqrt {V(1)^2+V(3)^2}} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} \end{bmatrix} \begin{bmatrix} \frac {K(1)} {\sqrt {K(1)^2+K(2)^2}} & -\frac {K(2)} {\sqrt {K(1)^2+K(2)^2}} & 0 \\ \frac {K(2)} {\sqrt {K(1)^2+K(2)^2}} & \frac {K(1)} {\sqrt {K(1)^2+K(2)^2}} & 0 \\ 0 & 0 & 1 \end{bmatrix}</math> | ||
#<math>E(1) \leftarrow \frac {\sqrt{\frac{\mu_2}{\varepsilon_2}} \cos \varphi - \sqrt{\frac{\mu_1}{\varepsilon_1}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi}} {\sqrt{\frac{\mu_2}{\varepsilon_2}} \cos \varphi + \sqrt{\frac{\mu_1}{\varepsilon_1}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi}}E(1)</math> | #<math>E(1) \leftarrow \frac {\sqrt{\frac{\mu_2}{\varepsilon_2}} \cos \varphi - \sqrt{\frac{\mu_1}{\varepsilon_1}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi}} {\sqrt{\frac{\mu_2}{\varepsilon_2}} \cos \varphi + \sqrt{\frac{\mu_1}{\varepsilon_1}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi}}E(1)</math> | ||
#<math>E(2) \leftarrow \frac {\sqrt{\frac{\mu_2}{\varepsilon_2}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi} - \sqrt{\frac{\mu_1}{\varepsilon_1}} \cos \varphi} {\sqrt{\frac{\mu_2}{\varepsilon_2}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi} + \sqrt{\frac{\mu_1}{\varepsilon_1}} \cos \varphi}E(2)</math> | #<math>E(2) \leftarrow \frac {\sqrt{\frac{\mu_2}{\varepsilon_2}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi} - \sqrt{\frac{\mu_1}{\varepsilon_1}} \cos \varphi} {\sqrt{\frac{\mu_2}{\varepsilon_2}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi} + \sqrt{\frac{\mu_1}{\varepsilon_1}} \cos \varphi}E(2)</math> | ||
#<math> | #<math>E \leftarrow \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos (180 - 2 \varphi) & \sin (180 - 2 \varphi) \\ 0 & -\sin (180 - 2 \varphi) & \cos (180 - 2 \varphi) \end{bmatrix} \begin{bmatrix} E(1) \\ E(2) \\ E(3) \end{bmatrix}</math> | ||
#<math>E \leftarrow \begin{bmatrix} E(1) & E(2) & E(3) \end{bmatrix} \begin{bmatrix} \frac {K(1)} {\sqrt {K(1)^2+K(2)^2}} & \frac {K(2)} {\sqrt {K(1)^2+K(2)^2}} & 0 \\ -\frac {K(2)} {\sqrt {K(1)^2+K(2)^2}} & \frac {K(1)} {\sqrt {K(1)^2+K(2)^2}} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac {\sqrt {V(1)^2+V(3)^2}} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} & -\frac {V(2)} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} \\ 0 & \frac {V(2)} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} & \frac {\sqrt {V(1)^2+V(3)^2}} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} \end{bmatrix} \begin{bmatrix} \frac {V(3)} {\sqrt {V(1)^2+V(3)^2}} & 0 & -\frac {V(1)} {\sqrt {V(1)^2+V(3)^2}} \\ 0 & 1 & 0 \\ \frac {V(1)} {\sqrt {V(1)^2+V(3)^2}} & 0 & \frac {V(3)} {\sqrt {V(1)^2+V(3)^2}} \end{bmatrix}</math> | |||
Версия 02:35, 27 мая 2017
Трехкомпонентный комплексный вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E} =\begin{pmatrix} \dot E_{x} \\ \dot E_{y} \\ \dot E_{z}\end{pmatrix}}
Функции
Уменьшить по пробегу(Напряженность, Пробег, Погонное затухание)
Изменить по отражению(Напряженность, КДП_1*, КМП_1**, КДП_2, КМП_2, Угол, Вектор(Направление луча), Вектор(Нормаль грани))
* - комплексная диэлектрическая проницаемость, ** - комплексная магнитная проницаемость.
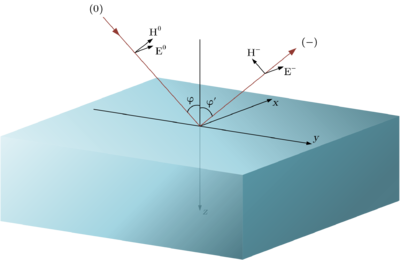
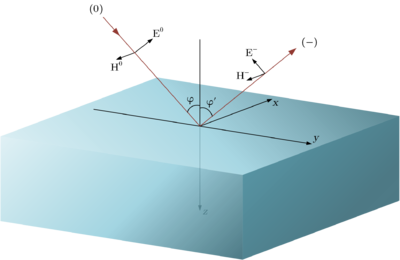
Пусть имеется граница раздела двух сред:
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left \{ \dot \varepsilon_1,~\dot \mu_1,~\dot k_1,~\dot W_1 \right \},~z<0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left \{ \dot \varepsilon_2,~\dot \mu_1,~\dot k_2,~\dot W_2 \right \},~z>0}
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \varepsilon = \varepsilon - i \frac{\sigma}{\omega}} - комплексная диэлектрическая проницаемость, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon} - диэлектрическая проницаемость среды,
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \sigma - проводимость среды
- - круговая частота волны
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mu} - магнитная проницаемость
При учете инерционности поляризации и намагничивания вводятся следующие комплексные проницаемости:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \varepsilon = \varepsilon \cos \alpha - i ( \frac{\sigma}{\omega} + \varepsilon \sin \alpha)}
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \mu = \mu \cos \beta - i \mu \sin \beta} , где
- - угол диэлектрических потерь
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \beta - угол магнитных потерь
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot k = \omega \sqrt{\dot \varepsilon \dot \mu}} - комплексное волновое число
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot W = \sqrt{\frac{\dot \mu}{\dot \varepsilon}}} - комплексное волновое сопротивление
Коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля):
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \rho_{\bot} = \frac {\dot W_2 \cos \varphi - \dot W_1 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi}} {\dot W_2 \cos \varphi + \dot W_1 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi}}}
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \rho_{\|} = \frac {\dot W_2 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi} - \dot W_1 \cos \varphi} {\dot W_2 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi} + \dot W_1 \cos \varphi}} , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi - угол падения
Таким образом отраженная волна имеет вид Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec {\dot E^-}=\vec {\dot E_{\bot}^-}+\vec {\dot E_{\|}^-}=\dot \rho_{\bot} \vec {\dot E_{\bot}^0}+\dot \rho_{\|} \vec {\dot E_{\|}^0}}
Т.к. напряженность поля дана в виде трехкомпонентного вектора относительно глобальной системы координат, необходимо найти параллельную и перпендикулярную составляющие соответственно данной грани и падающему лучу. Для этого составим матрицы поворота координатных осей таким образом, чтобы ось z совпала с направляющим вектором луча, а ось x с вектором векторного произведения направляющего вектора луча и вектора нормали грани. В результате в новых координатах .
На вход функции подается трехкомпонентный комплексный вектор напряженности, комплексные диэлектрические и магнитные проницаемости обоих сред, причем первыми даются характеристики среды из которой пришел луч. Также на вход функции поступает угол падения, направляющий вектор луча и вектор нормали грани. На выходе получаем трехкомпонентный вектор отраженной напряженности в глобальных координатах.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V\leftarrow} Вектор(Направление луча)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle N\leftarrow} Вектор(Нормаль грани)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E \leftarrow} Напряженность
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varphi \leftarrow} Угол
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon_1 \leftarrow} КДП_1
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon_2 \leftarrow} КДП_2
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mu_1 \leftarrow} КМП_1
- КМП_2
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle K \leftarrow N \times V}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E \leftarrow \begin{bmatrix} E(1) & E(2) & E(3) \end{bmatrix} \begin{bmatrix} \frac {V(3)} {\sqrt {V(1)^2+V(3)^2}} & 0 & \frac {V(1)} {\sqrt {V(1)^2+V(3)^2}} \\ 0 & 1 & 0 \\ -\frac {V(1)} {\sqrt {V(1)^2+V(3)^2}} & 0 & \frac {V(3)} {\sqrt {V(1)^2+V(3)^2}} \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac {\sqrt {V(1)^2+V(3)^2}} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} & \frac {V(2)} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} \\ 0 & -\frac {V(2)} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} & \frac {\sqrt {V(1)^2+V(3)^2}} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} \end{bmatrix} \begin{bmatrix} \frac {K(1)} {\sqrt {K(1)^2+K(2)^2}} & -\frac {K(2)} {\sqrt {K(1)^2+K(2)^2}} & 0 \\ \frac {K(2)} {\sqrt {K(1)^2+K(2)^2}} & \frac {K(1)} {\sqrt {K(1)^2+K(2)^2}} & 0 \\ 0 & 0 & 1 \end{bmatrix}}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E(1) \leftarrow \frac {\sqrt{\frac{\mu_2}{\varepsilon_2}} \cos \varphi - \sqrt{\frac{\mu_1}{\varepsilon_1}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi}} {\sqrt{\frac{\mu_2}{\varepsilon_2}} \cos \varphi + \sqrt{\frac{\mu_1}{\varepsilon_1}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi}}E(1)}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E(2) \leftarrow \frac {\sqrt{\frac{\mu_2}{\varepsilon_2}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi} - \sqrt{\frac{\mu_1}{\varepsilon_1}} \cos \varphi} {\sqrt{\frac{\mu_2}{\varepsilon_2}} \sqrt{ 1 - \frac {\mu_1 \varepsilon_1} {\mu_2 \varepsilon_2} \sin^2 \varphi} + \sqrt{\frac{\mu_1}{\varepsilon_1}} \cos \varphi}E(2)}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E \leftarrow \begin{bmatrix} E(1) & E(2) & E(3) \end{bmatrix} \begin{bmatrix} \frac {K(1)} {\sqrt {K(1)^2+K(2)^2}} & \frac {K(2)} {\sqrt {K(1)^2+K(2)^2}} & 0 \\ -\frac {K(2)} {\sqrt {K(1)^2+K(2)^2}} & \frac {K(1)} {\sqrt {K(1)^2+K(2)^2}} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac {\sqrt {V(1)^2+V(3)^2}} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} & -\frac {V(2)} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} \\ 0 & \frac {V(2)} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} & \frac {\sqrt {V(1)^2+V(3)^2}} {\sqrt {V(1)^2+V(2)^2+V(3)^2}} \end{bmatrix} \begin{bmatrix} \frac {V(3)} {\sqrt {V(1)^2+V(3)^2}} & 0 & -\frac {V(1)} {\sqrt {V(1)^2+V(3)^2}} \\ 0 & 1 & 0 \\ \frac {V(1)} {\sqrt {V(1)^2+V(3)^2}} & 0 & \frac {V(3)} {\sqrt {V(1)^2+V(3)^2}} \end{bmatrix}}
 - круговая частота волны
- круговая частота волны - угол диэлектрических потерь
- угол диэлектрических потерь .
.
 КМП_2
КМП_2