Распространение радиоволн ВЧ/Луч: различия между версиями
Nigiluk (обсуждение | вклад) |
Nigiluk (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
=Свойства луча= | =Свойства луча= | ||
# <tt>Начало()</tt>; | # <tt>Начало()</tt>; | ||
# <tt>Направление()</tt>; | # <tt>Направление()</tt>; | ||
=Функции= | =Функции= | ||
==<tt>Пересечение (Плоскость)</tt>== | ==<tt>Пересечение (Плоскость)</tt>== | ||
| Строка 26: | Строка 9: | ||
На вход функции принимается плоскость, задаваемая точкой <math>P_{face}</math> и вектором нормали <math>V_{face}</math>. Луч как геометрический объект определяется начальной точкой <math>P_{ray}</math> и вектором направления <math>V_{ray}</math>. | На вход функции принимается плоскость, задаваемая точкой <math>P_{face}</math> и вектором нормали <math>V_{face}</math>. Луч как геометрический объект определяется начальной точкой <math>P_{ray}</math> и вектором направления <math>V_{ray}</math>. | ||
#<math>P_{face} | #<math>P_{face}\leftarrow</math> <tt>Плоскость.Точка()</tt> | ||
#<math>P_{ray} \leftarrow</math> <tt>Начало()</tt> | #<math>V_{face}\leftarrow</math> <tt>Плоскость.Нормаль()</tt> | ||
#<math>V_{ray} \leftarrow</math> <tt>Направление()</tt> | #<math>P_{ray} \leftarrow</math> <tt>Луч.Начало()</tt> | ||
#<math>V_{ray} \leftarrow</math> <tt>Луч.Направление()</tt> | |||
#<math>P \leftarrow</math> (NaN, NaN, NaN) | #<math>P \leftarrow</math> (NaN, NaN, NaN) | ||
#Если <math>V_{face} \cdot V_{ray} \ne 0</math> | #Если <math>V_{face} \cdot V_{ray} \ne 0</math> | ||
##<math>t \leftarrow \frac {V_{face} \cdot P_{face} - V_{face} \cdot P_{ray}} {V_{face} \cdot V_{ray}}</math> | ##<math>t \leftarrow \frac {V_{face} \cdot P_{face} - V_{face} \cdot P_{ray}} {V_{face} \cdot V_{ray}}</math> | ||
##Если <math>t | ##Если <math>t > 0</math> | ||
###<math>P \leftarrow P_{ray} + t*V_{ray}</math> | ###<math>P \leftarrow P_{ray} + t*V_{ray}</math> | ||
#ВЫХОД | #ВЫХОД | ||
:Прим. "<math>\cdot</math>" здесь скалярное произведение, "<math>*</math>" произведение отдельно для каждой координаты | :Прим. "<math>\cdot</math>" здесь скалярное произведение, "<math>*</math>" произведение отдельно для каждой координаты. | ||
==<tt>Угол пересечения(Плоскость)</tt>== | ==<tt>Угол пересечения(Плоскость)</tt>== | ||
Возвращает угол падения луча на плоскость. | Возвращает угол падения луча на плоскость. | ||
На вход функции принимается плоскость, задаваемая вектором нормали <math>V_{face}</math>, луч определяется вектором направления <math>V_{ray}</math>. | |||
#<math>V_{face}\leftarrow</math> <tt>Плоскость.Нормаль()</tt> | |||
==<tt> | #<math>V_{ray} \leftarrow</math> <tt>Луч.Направление()</tt> | ||
#<math>\gamma \leftarrow \arcsin V_{face} \cdot V_{ray}</math> | |||
Если <math>\gamma>0</math> , то луч падает на "внутреннюю" сторону плоскости, если <math>\gamma<0</math> - на "внешнюю", если <math>\gamma=0</math> - луч параллелен плоскости. | |||
==<tt>Пробег(Точка)</tt>== | |||
Возвращает расстояние, пройденное лучом от начала до точки. | |||
#<math>P_{ray} \leftarrow</math> <tt>Луч.Начало()</tt> | |||
#<math>P \leftarrow</math> <tt>Точка</tt> | |||
#<math>r \leftarrow \left | P-P_{ray} \right |</math> | |||
Текущая версия на 22:17, 13 марта 2017
Свойства луча
- Начало();
- Направление();
Функции
Пересечение (Плоскость)
Возвращает точку пересечения луча с плоскостью.
На вход функции принимается плоскость, задаваемая точкой Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P_{face}} и вектором нормали Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_{face}} . Луч как геометрический объект определяется начальной точкой Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P_{ray}} и вектором направления .
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P_{face}\leftarrow} Плоскость.Точка()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_{face}\leftarrow} Плоскость.Нормаль()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P_{ray} \leftarrow} Луч.Начало()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_{ray} \leftarrow} Луч.Направление()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow (NaN, NaN, NaN)
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_{face} \cdot V_{ray} \ne 0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle t \leftarrow \frac {V_{face} \cdot P_{face} - V_{face} \cdot P_{ray}} {V_{face} \cdot V_{ray}}}
- Если
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P \leftarrow P_{ray} + t*V_{ray}}
- ВЫХОД
- Прим. "Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \cdot " здесь скалярное произведение, "Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle *} " произведение отдельно для каждой координаты.
Угол пересечения(Плоскость)
Возвращает угол падения луча на плоскость.
На вход функции принимается плоскость, задаваемая вектором нормали Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_{face}} , луч определяется вектором направления Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_{ray}} .
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_{face}\leftarrow} Плоскость.Нормаль()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_{ray} \leftarrow} Луч.Направление()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \gamma \leftarrow \arcsin V_{face} \cdot V_{ray}}
Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \gamma>0} , то луч падает на "внутреннюю" сторону плоскости, если - на "внешнюю", если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \gamma=0} - луч параллелен плоскости.
Пробег(Точка)
Возвращает расстояние, пройденное лучом от начала до точки.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P_{ray} \leftarrow} Луч.Начало()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow Точка
 .
.
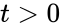
 - на "внешнюю", если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \gamma=0}
- луч параллелен плоскости.
- на "внешнюю", если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \gamma=0}
- луч параллелен плоскости.
