Распространение радиоволн ВЧ/Рей-трейсинг: различия между версиями
| (не показаны 34 промежуточные версии 2 участников) | |||
| Строка 17: | Строка 17: | ||
Шаги <math>\Delta_{\theta}\left(\theta\right)</math> по азимуту и <math>\Delta_{\varphi}\left(\varphi\right)</math> по зениту источника являются функциями от направления либо постоянными. | Шаги <math>\Delta_{\theta}\left(\theta\right)</math> по азимуту и <math>\Delta_{\varphi}\left(\varphi\right)</math> по зениту источника являются функциями от направления либо постоянными. | ||
==Угловой шаг дискретизации как функция ХН== | |||
[[Файл:Antenna pattern.png|400px|thumb|right|Диаграмма направленности и испускаемые моделью лучи]] | [[Файл:Antenna pattern.png|400px|thumb|right|Диаграмма направленности и испускаемые моделью лучи]] | ||
[[Файл:Antenna pattern (angular step).png|400px|thumb|right|Зависимость углового шага от азимутального угла]] | [[Файл:Antenna pattern (angular step).png|400px|thumb|right|Зависимость углового шага от азимутального угла]] | ||
Большинство современных вещательных систем используют панельные антенны с ограниченными углами раствора диаграммы направленности (ДН) в горизонтальной плоскости (до 120°) и очень малыми углами в вертикальной плоскости (до 20°). Соответственно, в таких системах происходит серьезное перераспределение излучаемой энергии в пространстве. Типичные коэффициенты усиления: 16-18 dBi. Поэтому одним из решений задачи оптимизации является использование динамического углового шага дискретизации <math>\Delta_{\theta},~\Delta_{\varphi}</math> как функции от характеристики направленности источника. | Большинство современных вещательных систем используют панельные антенны с ограниченными углами раствора диаграммы направленности (ДН) в горизонтальной плоскости (до 120°) и очень малыми углами в вертикальной плоскости (до 20°). Соответственно, в таких системах происходит серьезное перераспределение излучаемой энергии в пространстве. Типичные коэффициенты усиления: 16-18 dBi. Поэтому одним из решений задачи оптимизации является использование динамического углового шага дискретизации <math>\Delta_{\theta},~\Delta_{\varphi}</math> как функции от характеристики направленности источника. | ||
Изменение частоты дискретизации <math>\omega(\theta,\varphi)</math> происходит по следующему закону: | Изменение частоты дискретизации <math>\omega(\theta,\varphi, f)</math> происходит по следующему закону: | ||
<math>\omega(\theta,\varphi) = \ | <math>\omega(\theta,\varphi, f) = \omega_{min} + k F(\theta,\varphi, f)</math> , где | ||
:<math>k = \omega_{max} - \omega_{min}</math> - коэффициент девиации, где | :<math>k = \omega_{max} - \omega_{min}</math> - коэффициент девиации, где | ||
:<math>\omega_{max} = \frac{1}{\arcsin\left(\frac{\lambda}{R_{max}}\right)}\approx\frac{R_{max}}{\lambda}</math> - максимальное и <math>\omega_{min} = \alpha\omega_{max}</math> (для любого <math>0 \leq \alpha \leq 1</math>) минимальное значение частоты дискретизации; | |||
:<math>R_{max}</math> - максимальное расстояние от источника до границ модели; | |||
:<math>F</math> - функция ХН; | :<math>F</math> - функция ХН; | ||
:<math>\theta,~ \varphi</math> - | :<math>\theta,~ \varphi</math> - угол места и азимутальный угол; | ||
:<math>f</math> - частота излучения; | |||
:<math>\lambda</math> - длина излучаемой волны. | |||
Тогда шаг дискретизации (угол) будет меняться по следующим образом: | Тогда шаг дискретизации (угол) будет меняться по следующим образом: | ||
| Строка 57: | Строка 60: | ||
::<math>\frac{dn}{dh}=grad~n</math> - изменение коэффициента преломления с высотой. | ::<math>\frac{dn}{dh}=grad~n</math> - изменение коэффициента преломления с высотой. | ||
:<math>r=\sqrt{x^{2}+y^{2}}</math> - расстояние до точки с высотой <math>h(x,y)</math>. | :<math>r=\sqrt{x^{2}+y^{2}}</math> - расстояние до точки с высотой <math>h(x,y)</math>. | ||
==Основной цикл программы | Вариант 1== | ==Основной цикл программы | Вариант 1== | ||
| Строка 71: | Строка 73: | ||
##<math>\forall ~ \omega_n \in</math><tt> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].[[Распространение радиоволн ВЧ/Тип антенны|Тип антенны()]].[[Распространение радиоволн ВЧ/Амплитудно-частотная характеристика|Амплитудно-частотная характеристика()]]</tt> | ##<math>\forall ~ \omega_n \in</math><tt> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].[[Распространение радиоволн ВЧ/Тип антенны|Тип антенны()]].[[Распространение радиоволн ВЧ/Амплитудно-частотная характеристика|Амплитудно-частотная характеристика()]]</tt> | ||
###<math>\theta \leftarrow 0</math> | ###<math>\theta \leftarrow 0</math> | ||
###<math> | ###<math>\zeta_{\theta} \leftarrow 0</math> | ||
###Если <math>\theta < \pi \wedge (i=0 \vee \zeta_{\theta} \bmod 2 \neq 0)</math> | |||
####<math>\varphi \leftarrow 0</math> | |||
####<math>\zeta_{\varphi} \leftarrow 0</math> | |||
####Если <math>\varphi<2\pi \wedge (i=0 \vee \zeta_{\varphi} \bmod 2 \neq 0)</math> | |||
#####Position <math>\leftarrow</math> <tt> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].Позиция()</tt> | |||
#####Ray <math>\leftarrow</math><tt> [[Распространение радиоволн ВЧ/Луч|Луч()]].Создать(Position, [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].Мировая система координат(Вектор<math>(\theta,~\varphi, 1)</math>))</tt> | |||
#####Distance <math>\leftarrow \infty</math> | |||
#####<math>\forall ~ f_m\in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].Множество отражающих объектов()</tt> | |||
######<math>\forall ~ t_{mn} \in f_m</math><tt>.Множество отражающих поверхностей()</tt> | |||
#######<tt><math>P' \leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Пересечение([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость грани())</tt> | |||
#######Если <tt>[[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Принадлежность(<math>P'</math>)</tt> | |||
########Distance' <math>\leftarrow</math><tt> Расстояние(Position, <math>P'</math>)</tt> | |||
########Если Distance' <math><</math> Distance | |||
#########Distance <math>\leftarrow</math> Distance' | |||
#########<math>t' \leftarrow t_{mn}</math> | |||
#########<math>P \leftarrow P'</math> | |||
#####<math>\forall ~ \rho_k \in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Множество контрольных точек|Множество контрольных точек()]]</tt> | |||
######Если <math>\rho_k \in </math><tt> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].Область регистрации луча <math>(\theta,~\varphi,~\frac{\Delta_{\theta} (\theta)}{2^i},~\frac{\Delta_{\varphi} (\theta, \varphi)}{2^i},</math> Distance<math>)</math></tt> | |||
#######<tt><math>\rho_k</math>.Зарегистрировать([[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].Напряженность<math>(\omega_n,~\theta,~\varphi</math>, Расстояние(Position, <math>\rho_k</math>.Позиция()), [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]]<math>)</math>)</tt> | |||
#####Если <tt>[[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].Напряженность<math>(\omega_n,~\theta,~\varphi</math>, Distance, [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]]</tt><math>)>E_{end}</math> | |||
######Angle <tt><math>\leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Угол пересечения([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t'</math>]].Плоскость грани())</tt> | |||
######<math>s' \leftarrow</math><tt> [[Распространение радиоволн ВЧ/Вторичный источник при рейтрейсинге|Вторичный источник при рейтрейсинге]].Создать([[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].Напряженность<math>(\omega_n,~\theta,~\varphi</math>, Distance, [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]]<math>),</math> Angle, <math>P,~t'</math>)</tt> | |||
######<math>S \leftarrow S \cup \{s'\}</math> | |||
####<math>\varphi \leftarrow \varphi + \frac{\Delta_{\varphi} (\theta, \varphi)}{2^i}</math> | |||
####<math>\theta \leftarrow \theta + \frac{\Delta_{\theta} (\theta)}{2^i}</math> | ####<math>\zeta_{\varphi} \leftarrow \zeta_{\varphi}+1</math> | ||
###<math>\theta \leftarrow \theta + \frac{\Delta_{\theta} (\theta)}{2^i}</math> | |||
###<math>\zeta_{\theta} \leftarrow \zeta_{\theta}+1</math> | |||
#Переход на шаг 2 | #Переход на шаг 2 | ||
| Строка 104: | Строка 108: | ||
==Основной цикл программы | Вариант 2== | ==Основной цикл программы | Вариант 2== | ||
'''Геометрическая модель (рей-трейсинг 2)'''. | |||
''Наследует свойства [[Распространение радиоволн ВЧ/Геометрическая модель|Геометрической модели]].'' | |||
* Предикат завершения(). При <math>i = 0</math> возвращает истину, иначе возвращает значение функции SubApprox для результатов моделирования не предыдущем и на текущем этапах, а также для включаемого отклонения <math>\Delta</math> и допустимого процента точек <math>k</math>. | |||
===Предусловия=== | ===Предусловия=== | ||
<math>G</math> - входное описание среды распространения моделируемого поля, заданное [[Распространение радиоволн ВЧ/Геометрическая модель|геометрической моделью]]. | * <math>G</math> - входное описание среды распространения моделируемого поля, заданное [[Распространение радиоволн ВЧ/Геометрическая модель|геометрической моделью]]. | ||
* <math>\Omega</math> - список частот, на которых необходимо провести моделирование. | |||
* <math>E_{end}</math> - критическое значение напряженности, на котором дальнейшая трассировка луча прекращается. | |||
* <math>\Delta</math> - критерий разности между текущим и предыдущим результатом моделирования, при которой можно считать, что поле промоделированно точно. | |||
===Основное течение=== | ===Основное течение=== | ||
#<math>\forall ~ s_j \in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Первичный источник| | #<math>\forall ~ \omega_n \in \Omega</math> | ||
##<math>\forall ~ \ | ##<math>i \leftarrow 0</math> | ||
##Pre_SCP <math> \leftarrow</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Множество контрольных точек|Множество контрольных точек(<math>\omega_n</math>)]]</tt> ''//Копирование состояния до изменения''. | |||
##Set_event <math>\leftarrow</math><tt> Preprocessing(<math>G,~i,~\omega_n</math>)</tt> | |||
##<math>\forall ~ (s_j,~\theta,~\varphi) \in </math> Set_event | |||
###Ray <math>\leftarrow</math><tt> [[Распространение радиоволн ВЧ/Луч|Луч()]].Создать([[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]], <math>\theta,~\varphi,~\omega_n</math>)</tt> | |||
###<tt>Trace(Ray, [[Распространение радиоволн ВЧ/Геометрическая модель|G]], <math>E_{end}</math>)</tt> | |||
##<tt>Postprocessing([[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Множество контрольных точек|Множество контрольных точек(<math>\omega_n</math>)]])</tt> | |||
##SAcheck <math>\leftarrow</math><tt> SucApprox([[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Множество контрольных точек|Множество контрольных точек(<math>\omega_n</math>)]], Pre_SCP, <math>\Delta</math>)</tt> | |||
##Если SAcheck | |||
###<math>i \leftarrow i+1</math> | |||
###Переход на 1.2 | |||
#ВЫХОД | |||
===<tt>[Таблица событий] <math>\leftarrow</math> Preprocessing(Геометрическая модель, Номер итерации, Частота)</tt>=== | |||
Функция создает таблицу событий, необходимых обработать. В качестве событий - испускаемые моделью лучи на данной частоте. | |||
#<math>T \leftarrow</math> Пустой односвязный список значений <math>(s_j,~\theta,~\varphi)</math>. | |||
#<math>G \leftarrow</math> Геометрическая модель. | |||
#<math>i \leftarrow</math> Номер итерации | |||
#<math>\omega \leftarrow</math> Частота | |||
#<math>\forall ~ s_j \in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Первичный источник|Множество первичных источников()]]</tt> | |||
##Если <tt> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].[[Распространение радиоволн ВЧ/Тип антенны|Тип антенны()]].[[Распространение радиоволн ВЧ/Амплитудно-частотная характеристика|Амплитудно-частотная характеристика(<math>\omega</math>)]]</tt> <math>\ne 0</math> | |||
###<math>\theta \leftarrow 0</math> | |||
###<math>\zeta_{\theta} \leftarrow 0</math> | |||
###Пока <math>\theta < \pi</math> | |||
####<math>\varphi \leftarrow 0</math> | |||
####<math>\zeta_{\varphi} \leftarrow 0</math> | |||
####Пока <math>\varphi<2\pi</math> | |||
#####Если <math>i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0</math> | |||
######<math>T</math>.Добавить<math>(s_j,~\theta,~\varphi)</math> | |||
#####<math>\varphi \leftarrow \varphi + \frac{\Delta_{\varphi} (s_j,~\theta,~\varphi)}{2^i}</math> | |||
#####<math>\zeta_{\varphi} \leftarrow \zeta_{\varphi}+1</math> | |||
####<math>\theta \leftarrow \theta + \frac{\Delta_{\theta} (s_j,~\theta)}{2^i}</math> | |||
####<math>\zeta_{\theta} \leftarrow \zeta_{\theta}+1</math> | |||
#Вернуть Массив(<math>T</math>) | |||
Если <math>\Delta_{\varphi} (s_j,~\theta,~\varphi) = {\rm const}</math>, и <math>\Delta_{\theta} (s_j,~\theta) = {\rm const}</math>, то есть углы распределены равномерно, таблица может быть реализована в виде массива значений <math>(s_j,~\theta,~\varphi)</math>, элементы которого могут заполняться параллельно, без синхронизации. Если же размер таблицы заранее не определен (общий случай), то таблица реализуется связанным списком, добавление элементов в который должно защищаться мьютексом на шаге 4.1.3.1.3.1.1, а алгоритм на заключительном шаге преобразует связанный список в массив с произвольным доступом. Второй путь при параллельном выполнении - создавать таблицы в локальной памяти потока, после выполнения которых - объединять таблицы в массив в основном потоке. | |||
====Параллельная форма==== | |||
Параллельное выполнение в общем случае возможно только цикла, перебирающего первичные источники (шаг 4), так как распределение углов заранее не определено. | |||
Пусть <math>P>0</math> - число потоков, выполняющих функцию. Пусть <math>T'</math> - массив изначально пустых связанных списков троек <math>(s_j,~\theta,~\varphi)</math>, так, что <math>T'_i</math> - <math>i</math>-тый список массива, <math>0\le i<P</math>. | |||
#<math>i \leftarrow</math> Номер итерации | |||
#<math>\omega \leftarrow</math> Частота | |||
#<math>T'\leftarrow</math>Создать массив. | |||
#<math>\forall ~ s_j \in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Первичный источник|Множество первичных источников()]]</tt> | |||
##<math>t\leftarrow</math> индекс потока. | |||
##Если <tt> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].[[Распространение радиоволн ВЧ/Тип антенны|Тип антенны()]].[[Распространение радиоволн ВЧ/Амплитудно-частотная характеристика|Амплитудно-частотная характеристика(<math>\omega</math>)]]</tt> <math>\ne 0</math> | |||
###<math>\theta \leftarrow 0</math> | ###<math>\theta \leftarrow 0</math> | ||
###<math> | ###<math>\zeta_{\theta} \leftarrow 0</math> | ||
### | ###Пока <math>\theta < \pi</math> | ||
####<math>\varphi \leftarrow 0</math> | |||
####<math>\zeta_{\varphi} \leftarrow 0</math> | |||
####Пока <math>\varphi<2\pi</math> | |||
#####Если <math>i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0</math> | |||
##### | ######<math>T'_t</math>.Добавить<math>(s_j,~\theta,~\varphi)</math> | ||
#### | #####<math>\varphi \leftarrow \varphi + \frac{\Delta_{\varphi} (s_j,~\theta,~\varphi)}{2^i}</math> | ||
# | #####<math>\zeta_{\varphi} \leftarrow \zeta_{\varphi}+1</math> | ||
####<math>\theta \leftarrow \theta + \frac{\Delta_{\theta} (s_j,~\theta)}{2^i}</math> | |||
####<math>\zeta_{\theta} \leftarrow \zeta_{\theta}+1</math> | |||
#Вернуть Массив<math>\left(\bigsqcup_{t=0}^{P-1}T'_t\right)</math> | |||
#### | ===<tt>Trace</tt>=== | ||
Функция трассирует луч через геометрическую модель и и фиксирует его прохождение вблизи контрольной точки. | |||
##### | |||
#<math>R\leftarrow \infty</math> | |||
#<math>T\leftarrow </math> NaN | |||
#<math>\forall ~ f_m\in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].Множество отражающих объектов()</tt> | |||
## | ##<math>\forall ~ t_{mn} \in f_m</math><tt>.Множество отражающих поверхностей()</tt> | ||
### | ###<tt><math>p \leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Пересечение([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость())</tt> | ||
#### | ###Если <tt>[[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Принадлежность(<math>p</math>)</tt> | ||
## | ####<math>r\leftarrow</math><tt> [[Распространение радиоволн ВЧ/Луч|Ray]].Пробег(<math>p</math>)</tt> | ||
####Если <math>r < R</math> | |||
## | #####<math>R \leftarrow r</math> | ||
#####<math>T \leftarrow t_{mn}</math> | |||
#####<math>P \leftarrow p</math> | |||
#<math>\forall ~ O_k \in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Плоскость вывода результатов|Множество плоскостей вывода результатов()]]</tt> | |||
##<tt><math>p \leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Пересечение([[Распространение радиоволн ВЧ/Плоскость вывода результатов|<math>O_k</math>]].Плоскость())</tt> | |||
##Если <tt>[[Распространение радиоволн ВЧ/Плоскость вывода результатов|<math>O_k</math>]].Принадлежность(<math>p</math>)</tt> | |||
###<math>r\leftarrow</math><tt> [[Распространение радиоволн ВЧ/Луч|Ray]].Пробег(<math>p</math>)</tt> | |||
###Если <math>r < R</math> | |||
####<math>\rho \leftarrow</math><tt> [[Распространение радиоволн ВЧ/Плоскость вывода результатов|<math>O_k</math>]].Ближайшая контрольная точка(<math>p</math>)</tt> | |||
####<tt><math>\rho</math>.Зарегистрировать([[Распространение радиоволн ВЧ/Луч|Ray]], <math>r</math>, [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]])</tt> | |||
#Если <math>T \not\equiv</math> NaN | |||
##<tt><math>\gamma \leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Угол пересечения([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>T</math>]].Плоскость())</tt> | |||
##<tt>[[Распространение радиоволн ВЧ/Луч|Ray]].Отразить(<math>T,~P,~R,~\gamma</math>, [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]])</tt> | |||
##Если <tt>[[Распространение радиоволн ВЧ/Луч|Ray]].Напряженность <math> >E_{end} </math></tt> | |||
###<tt>Trace(Ray, [[Распространение радиоволн ВЧ/Геометрическая модель|G]], <math>E_{end}</math>)</tt> | |||
===<tt>Postprocessing</tt>=== | |||
Функция "проявляет" поле в контрольных точках по накопленным значениям напряженности от всех пришедших лучей. | |||
===<tt>SucApprox</tt>=== | |||
Функция сравнивает текущие результаты моделирования с результатами, полученными на предыдущем шаге. На выходе получаем флаг, по которому решаем, следует ли продолжать уточнять модель. | |||
===Свойства алгоритма=== | ===Свойства алгоритма=== | ||
====Сложность==== | ====Сложность==== | ||
====Возможности распараллеливания==== | ====Возможности распараллеливания==== | ||
<graphviz size=500px> | |||
digraph ray_tracing_EM_parallel_run{ | |||
rankdir=LR; | |||
node[fontsize=14]; | |||
edge[fontsize=14]; | |||
G0[label="ВХОД"]; | |||
G1[label="1"]; | |||
G2_1[label="2"]; | |||
G3_1[label="3"]; | |||
G4_1[label="4"]; | |||
G5_1[label="5"]; | |||
G2_2[label="2"]; | |||
G3_2[label="3"]; | |||
G4_2[label="4"]; | |||
G5_2[label="5"]; | |||
G6_1_1[label="6"]; | |||
G6_1_2[label="6"]; | |||
G6_2_1[label="6"]; | |||
G6_2_2[label="6"]; | |||
G7_1_1_1[label="7.1"]; | |||
G7_3_1_1[label="7.3"]; | |||
G7_4_1_1_1[label="7.4"]; | |||
G7_4_1_1_2[label="7.4"]; | |||
G7_5_1_1_1_1[label="7.5"]; | |||
G7_13_1_1_1_1[label="7.13"]; | |||
G7_5_1_1_1_2[label="7.5"]; | |||
G7_13_1_1_1_2[label="7.13"]; | |||
G7_5_1_1_2_1[label="7.5"]; | |||
G7_13_1_1_2_1[label="7.13"]; | |||
G7_5_1_1_2_2[label="7.5"]; | |||
G7_13_1_1_2_2[label="7.13"]; | |||
G7_14_1_1_1[label="7.14"]; | |||
G7_14_1_1_2[label="7.14"]; | |||
G7_15_1_1[label="7.15"]; | |||
G7_16_1_1[label="7.16"]; | |||
G7_17_1_1_1[label="7.17"]; | |||
G7_24_1_1_1[label="7.24"]; | |||
G7_17_1_1_2[label="7.17"]; | |||
G7_24_1_1_2[label="7.24"]; | |||
G7_25_1_1[label="7.25"]; | |||
G7_32_1_1[label="7.32"]; | |||
G7_1_1_2[label="7.1"]; | |||
G7_3_1_2[label="7.3"]; | |||
G7_4_1_2_1[label="7.4"]; | |||
G7_4_1_2_2[label="7.4"]; | |||
G7_5_1_2_1_1[label="7.5"]; | |||
G7_13_1_2_1_1[label="7.13"]; | |||
G7_5_1_2_1_2[label="7.5"]; | |||
G7_13_1_2_1_2[label="7.13"]; | |||
G7_5_1_2_2_1[label="7.5"]; | |||
G7_13_1_2_2_1[label="7.13"]; | |||
G7_5_1_2_2_2[label="7.5"]; | |||
G7_13_1_2_2_2[label="7.13"]; | |||
G7_14_1_2_1[label="7.14"]; | |||
G7_14_1_2_2[label="7.14"]; | |||
G7_15_1_2[label="7.15"]; | |||
G7_16_1_2[label="7.16"]; | |||
G7_17_1_2_1[label="7.17"]; | |||
G7_24_1_2_1[label="7.24"]; | |||
G7_17_1_2_2[label="7.17"]; | |||
G7_24_1_2_2[label="7.24"]; | |||
G7_25_1_2[label="7.25"]; | |||
G7_32_1_2[label="7.32"]; | |||
G7_1_2_1[label="7.1"]; | |||
G7_3_2_1[label="7.3"]; | |||
G7_4_2_1_1[label="7.4"]; | |||
G7_4_2_1_2[label="7.4"]; | |||
G7_5_2_1_1_1[label="7.5"]; | |||
G7_13_2_1_1_1[label="7.13"]; | |||
G7_5_2_1_1_2[label="7.5"]; | |||
G7_13_2_1_1_2[label="7.13"]; | |||
G7_5_2_1_2_1[label="7.5"]; | |||
G7_13_2_1_2_1[label="7.13"]; | |||
G7_5_2_1_2_2[label="7.5"]; | |||
G7_13_2_1_2_2[label="7.13"]; | |||
G7_14_2_1_1[label="7.14"]; | |||
G7_14_2_1_2[label="7.14"]; | |||
G7_15_2_1[label="7.15"]; | |||
G7_16_2_1[label="7.16"]; | |||
G7_17_2_1_1[label="7.17"]; | |||
G7_24_2_1_1[label="7.24"]; | |||
G7_17_2_1_2[label="7.17"]; | |||
G7_24_2_1_2[label="7.24"]; | |||
G7_25_2_1[label="7.25"]; | |||
G7_32_2_1[label="7.32"]; | |||
G7_1_2_2[label="7.1"]; | |||
G7_3_2_2[label="7.3"]; | |||
G7_4_2_2_1[label="7.4"]; | |||
G7_4_2_2_2[label="7.4"]; | |||
G7_5_2_2_1_1[label="7.5"]; | |||
G7_13_2_2_1_1[label="7.13"]; | |||
G7_5_2_2_1_2[label="7.5"]; | |||
G7_13_2_2_1_2[label="7.13"]; | |||
G7_5_2_2_2_1[label="7.5"]; | |||
G7_13_2_2_2_1[label="7.13"]; | |||
G7_5_2_2_2_2[label="7.5"]; | |||
G7_13_2_2_2_2[label="7.13"]; | |||
G7_14_2_2_1[label="7.14"]; | |||
G7_14_2_2_2[label="7.14"]; | |||
G7_15_2_2[label="7.15"]; | |||
G7_16_2_2[label="7.16"]; | |||
G7_17_2_2_1[label="7.17"]; | |||
G7_24_2_2_1[label="7.24"]; | |||
G7_17_2_2_2[label="7.17"]; | |||
G7_24_2_2_2[label="7.24"]; | |||
G7_25_2_2[label="7.25"]; | |||
G7_32_2_2[label="7.32"]; | |||
G8_1[label="8"]; | |||
G14_1[label="14"]; | |||
G8_2[label="8"]; | |||
G14_2[label="14"]; | |||
G15[label="15"]; | |||
SKIP_1[label="...", shape="none"]; | |||
SKIP_2[label="...", shape="none"]; | |||
SKIP_3[label="...", shape="none"]; | |||
SKIP_4[label="...", shape="none"]; | |||
SKIP_5[label="...", shape="none"]; | |||
SKIP_6[label="...", shape="none"]; | |||
SKIP_7[label="...", shape="none"]; | |||
SKIP_8[label="...", shape="none"]; | |||
SKIP_9[label="...", shape="none"]; | |||
SKIP_10[label="...", shape="none"]; | |||
//SKIP_11[label="...", shape="none"]; | |||
SKIP_12[label="...", shape="none"]; | |||
SKIP_13[label="...", shape="none"]; | |||
SKIP_14[label="...", shape="none"]; | |||
SKIP_15[label="...", shape="none"]; | |||
SKIP_16[label="...", shape="none"]; | |||
SKIP_17[label="...", shape="none"]; | |||
SKIP_18[label="...", shape="none"]; | |||
SKIP_19[label="...", shape="none"]; | |||
SKIP_20[label="...", shape="none"]; | |||
SKIP_21[label="...", shape="none"]; | |||
SKIP_22[label="...", shape="none"]; | |||
SKIP_23[label="...", shape="none"]; | |||
SKIP_24[label="...", shape="none"]; | |||
SKIP_25[label="...", shape="none"]; | |||
SKIP_26[label="...", shape="none"]; | |||
SKIP_27[label="...", shape="none"]; | |||
SKIP_28[label="...", shape="none"]; | |||
SKIP_29[label="...", shape="none"]; | |||
SKIP_30[label="...", shape="none"]; | |||
SKIP_31[label="...", shape="none"]; | |||
G0->G1->{G2_1, G2_2} | |||
G2_1->G3_1->G4_1->G5_1->{G6_1_1, G6_1_2} | |||
G6_1_1->G7_1_1_1 | |||
G6_1_2->G7_1_1_2 | |||
{G7_32_1_1, G7_32_1_2}->G8_1->SKIP_30->G14_1 | |||
G2_2->G3_2->G4_2->G5_2->{G6_2_1, G6_2_2} | |||
G6_2_1->G7_1_2_1 | |||
G6_2_2->G7_1_2_2 | |||
{G7_32_2_1, G7_32_2_2}->G8_2->SKIP_31->G14_2 | |||
{G14_1, G14_2}->G15->"ВЫХОД" | |||
G7_1_1_1->G7_3_1_1->{G7_4_1_1_1, G7_4_1_1_2} | |||
G7_4_1_1_1->{G7_5_1_1_1_1, G7_5_1_1_1_2} | |||
G7_5_1_1_1_1->SKIP_1->G7_13_1_1_1_1 | |||
G7_5_1_1_1_2->SKIP_2->G7_13_1_1_1_2 | |||
{G7_13_1_1_1_1, G7_13_1_1_1_2}->G7_14_1_1_1 | |||
G7_4_1_1_2->{G7_5_1_1_2_1, G7_5_1_1_2_2} | |||
G7_5_1_1_2_1->SKIP_3->G7_13_1_1_2_1 | |||
G7_5_1_1_2_2->SKIP_4->G7_13_1_1_2_2 | |||
{G7_13_1_1_2_1, G7_13_1_1_2_2}->G7_14_1_1_2 | |||
{G7_14_1_1_1, G7_14_1_1_2}->G7_15_1_1->G7_16_1_1->{G7_17_1_1_1, G7_17_1_1_2} | |||
G7_17_1_1_1->SKIP_5->G7_24_1_1_1 | |||
G7_17_1_1_2->SKIP_6->G7_24_1_1_2 | |||
{G7_24_1_1_1, G7_24_1_1_2}->G7_25_1_1->SKIP_15->G7_32_1_1 | |||
G7_1_1_2->G7_3_1_2->{G7_4_1_2_1, G7_4_1_2_2} | |||
G7_4_1_2_1->{G7_5_1_2_1_1, G7_5_1_2_1_2} | |||
G7_5_1_2_1_1->SKIP_18->G7_13_1_2_1_1 | |||
G7_5_1_2_1_2->SKIP_19->G7_13_1_2_1_2 | |||
{G7_13_1_2_1_1, G7_13_1_2_1_2}->G7_14_1_2_1 | |||
G7_4_1_2_2->{G7_5_1_2_2_1, G7_5_1_2_2_2} | |||
G7_5_1_2_2_1->SKIP_16->G7_13_1_2_2_1 | |||
G7_5_1_2_2_2->SKIP_17->G7_13_1_2_2_2 | |||
{G7_13_1_2_2_1, G7_13_1_2_2_2}->G7_14_1_2_2 | |||
{G7_14_1_2_1, G7_14_1_2_2}->G7_15_1_2->G7_16_1_2->{G7_17_1_2_1, G7_17_1_2_2} | |||
G7_17_1_2_1->SKIP_7->G7_24_1_2_1 | |||
G7_17_1_2_2->SKIP_8->G7_24_1_2_2 | |||
{G7_24_1_2_1, G7_24_1_2_2}->G7_25_1_2->SKIP_12->G7_32_1_2 | |||
G7_1_2_1->G7_3_2_1->{G7_4_2_1_1, G7_4_2_1_2} | |||
G7_4_2_1_1->{G7_5_2_1_1_1, G7_5_2_1_1_2} | |||
G7_5_2_1_1_1->SKIP_20->G7_13_2_1_1_1 | |||
G7_5_2_1_1_2->SKIP_21->G7_13_2_1_1_2 | |||
{G7_13_2_1_1_1, G7_13_2_1_1_2}->G7_14_2_1_1 | |||
G7_4_2_1_2->{G7_5_2_1_2_1, G7_5_2_1_2_2} | |||
G7_5_2_1_2_1->SKIP_22->G7_13_2_1_2_1 | |||
G7_5_2_1_2_2->SKIP_23->G7_13_2_1_2_2 | |||
{G7_13_2_1_2_1, G7_13_2_1_2_2}->G7_14_2_1_2 | |||
{G7_14_2_1_1, G7_14_2_1_2}->G7_15_2_1->G7_16_2_1->{G7_17_2_1_1, G7_17_2_1_2} | |||
G7_17_2_1_1->SKIP_9->G7_24_2_1_1 | |||
G7_17_2_1_2->SKIP_10->G7_24_2_1_2 | |||
{G7_24_2_1_1, G7_24_2_1_2}->G7_25_2_1->SKIP_13->G7_32_2_1 | |||
G7_1_2_2->G7_3_2_2->{G7_4_2_2_1, G7_4_2_2_2} | |||
G7_4_2_2_1->{G7_5_2_2_1_1, G7_5_2_2_1_2} | |||
G7_5_2_2_1_1->SKIP_24->G7_13_2_2_1_1 | |||
G7_5_2_2_1_2->SKIP_25->G7_13_2_2_1_2 | |||
{G7_13_2_2_1_1, G7_13_2_2_1_2}->G7_14_2_2_1 | |||
G7_4_2_2_2->{G7_5_2_2_2_1, G7_5_2_2_2_2} | |||
G7_5_2_2_2_1->SKIP_26->G7_13_2_2_2_1 | |||
G7_5_2_2_2_2->SKIP_27->G7_13_2_2_2_2 | |||
{G7_13_2_2_2_1, G7_13_2_2_2_2}->G7_14_2_2_2 | |||
{G7_14_2_2_1, G7_14_2_2_2}->G7_15_2_2->G7_16_2_2->{G7_17_2_2_1, G7_17_2_2_2} | |||
G7_17_2_2_1->SKIP_28->G7_24_2_2_1 | |||
G7_17_2_2_2->SKIP_29->G7_24_2_2_2 | |||
{G7_24_2_2_1, G7_24_2_2_2}->G7_25_2_2->SKIP_14->G7_32_2_2 | |||
} | |||
</graphviz> | |||
Текущая версия на 07:50, 14 февраля 2018
Модель
Алгоритм
Идея последовательного приближения
Идея заключается в последовательном удвоении числа элементарных модельных экспериментов. Это продолжится до тех пор, пока результат текущего моделирования не приблизится к результату моделирования на предыдущей итерации:
, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta - параметр моделирования, задаваемый пользователем.
Однако сравнение соседних итераций не дает достаточного условия на достижение заданной точности (основная причина этого - излучение по направлениям). Поэтому правильнее будет сравнивать итерации через одну, две и т.д.:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \left | F_i-F_{i-k} \right |<\Delta , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): k также будет задаваться пользователем.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i здесь - это параметр цикла, стоящего над циклами основной программы, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i=\overline{0:N} .
При равномерном увеличении числа направлений излучения от первичного источника в два раза путем деления на 2 соответствующего шага по углу в процессе увеличения Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i , только каждое второе направление будет новым, т.е. не учитанным на предыдущих итерациях. Другая половина будет повторять эксперименты, уже выполненные ранее. Поэтому в цикл основной программы введено дополнительное условие для учета этих повторений.
Шаги Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta_{\theta}\left(\theta\right) по азимуту и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta_{\varphi}\left(\varphi\right) по зениту источника являются функциями от направления либо постоянными.
Угловой шаг дискретизации как функция ХН
Большинство современных вещательных систем используют панельные антенны с ограниченными углами раствора диаграммы направленности (ДН) в горизонтальной плоскости (до 120°) и очень малыми углами в вертикальной плоскости (до 20°). Соответственно, в таких системах происходит серьезное перераспределение излучаемой энергии в пространстве. Типичные коэффициенты усиления: 16-18 dBi. Поэтому одним из решений задачи оптимизации является использование динамического углового шага дискретизации Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta_{\theta},~\Delta_{\varphi} как функции от характеристики направленности источника.
Изменение частоты дискретизации Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega(\theta,\varphi, f) происходит по следующему закону:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega(\theta,\varphi, f) = \omega_{min} + k F(\theta,\varphi, f) , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): k = \omega_{max} - \omega_{min} - коэффициент девиации, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_{max} = \frac{1}{\arcsin\left(\frac{\lambda}{R_{max}}\right)}\approx\frac{R_{max}}{\lambda} - максимальное и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_{min} = \alpha\omega_{max} (для любого Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): 0 \leq \alpha \leq 1 ) минимальное значение частоты дискретизации;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R_{max} - максимальное расстояние от источника до границ модели;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): F - функция ХН;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta,~ \varphi - угол места и азимутальный угол;
- - частота излучения;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \lambda - длина излучаемой волны.
Тогда шаг дискретизации (угол) будет меняться по следующим образом:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta_{\theta},~\Delta_{\varphi} = \frac {1} {\omega(\theta,\varphi)}
Общее кол-во лучей определяется выражением:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): N_{total} = \frac {1} {2 \pi^2} \int \limits_0^{\pi} \int \limits_0^{2 \pi} \omega(\theta,\varphi)~d \theta d \varphi
С учетом, что максимум ДН находится в Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta=0,~\varphi=0 , получим выражения:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): N_{\theta~total} = \frac {1} {\pi} \int \limits_0^{\pi} \omega(\theta,\varphi) \bigr|_{\varphi=0}~d \theta ,
Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): N_{\varphi~total}(\theta) = \frac {1} {2 \pi} \int \limits_0^{2 \pi} \omega(\theta,\varphi)~d \varphi .
Инициализация геометрической модели
Перерасчет высот с учетом кривизны земли и рефракции радиоволн в тропосфере.
Входной параметр пересчитывается в соответствии с формулой:
, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R_{eq}=\frac{R_0}{1+R_0 \frac{dn}{dh}}
- эквивалентный радиус Земли, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R_0=6371 - радиус Земли (км),
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \frac{dn}{dh}=grad~n - изменение коэффициента преломления с высотой.
- - расстояние до точки с высотой Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): h(x,y) .
Основной цикл программы | Вариант 1
Предусловия
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): G - входное описание среды распространения моделируемого поля, заданное геометрической моделью.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i - номер итерации моделирования, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i\geq 0 .
Основное течение
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \leftarrow G.Множество первичных источников()
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \colon ~\varnothing то ВЫХОД
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ s_j \in S
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \leftarrow S~ \backslash \left \{ s_j \right \}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ \omega_n \in
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Антенна().Тип антенны().Амплитудно-частотная характеристика()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta \leftarrow 0
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\theta} \leftarrow 0
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta < \pi \wedge (i=0 \vee \zeta_{\theta} \bmod 2 \neq 0)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi \leftarrow 0
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\varphi} \leftarrow 0
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi<2\pi \wedge (i=0 \vee \zeta_{\varphi} \bmod 2 \neq 0)
- Position Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Антенна().Позиция()
- Ray Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Луч().Создать(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Антенна().Мировая система координат(ВекторНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\theta,~\varphi, 1) ))
- Distance Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow \infty
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ f_m\in
G.Множество отражающих объектов()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P' \leftarrow Ray.Пересечение(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} .Плоскость грани())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn}
.Принадлежность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P'
)
- Distance' Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Расстояние(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P' )
- Если Distance' Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): <
Distance
- Distance Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Distance'
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t' \leftarrow t_{mn}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow P'
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ \rho_k \in
G.Множество контрольных точек()
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k \in
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Область регистрации луча Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\theta,~\varphi,~\frac{\Delta_{\theta} (\theta)}{2^i},~\frac{\Delta_{\varphi} (\theta, \varphi)}{2^i},
DistanceНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): )
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k .Зарегистрировать(.НапряженностьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\omega_n,~\theta,~\varphi , Расстояние(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k .Позиция()), G.Среда распространения()Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): ) )
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k \in
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Область регистрации луча Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\theta,~\varphi,~\frac{\Delta_{\theta} (\theta)}{2^i},~\frac{\Delta_{\varphi} (\theta, \varphi)}{2^i},
DistanceНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): )
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Напряженность, Distance, G.Среда распространения()
- Angle Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Ray.Угол пересечения(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t' .Плоскость грани())
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s' \leftarrow Вторичный источник при рейтрейсинге.Создать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .НапряженностьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\omega_n,~\theta,~\varphi , Distance, G.Среда распространения()Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): ), Angle, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): P,~t' )
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \leftarrow S \cup \{s'\}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \varphi \leftarrow \varphi + \frac{\Delta_{\varphi} (\theta, \varphi)}{2^i}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \zeta_{\varphi} \leftarrow \zeta_{\varphi}+1
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta \leftarrow \theta + \frac{\Delta_{\theta} (\theta)}{2^i}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \zeta_{\theta} \leftarrow \zeta_{\theta}+1
- Переход на шаг 2
Свойства алгоритма
Сложность
Возможности распараллеливания
Основной цикл программы | Вариант 2
Геометрическая модель (рей-трейсинг 2). Наследует свойства Геометрической модели.
- Предикат завершения(). При Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle i=0} возвращает истину, иначе возвращает значение функции SubApprox для результатов моделирования не предыдущем и на текущем этапах, а также для включаемого отклонения Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta и допустимого процента точек .
Предусловия
- - входное описание среды распространения моделируемого поля, заданное геометрической моделью.
- - список частот, на которых необходимо провести моделирование.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E_{end} - критическое значение напряженности, на котором дальнейшая трассировка луча прекращается.
- - критерий разности между текущим и предыдущим результатом моделирования, при которой можно считать, что поле промоделированно точно.
Основное течение
-
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i \leftarrow 0
- Pre_SCP Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \leftarrow } G.Множество контрольных точек(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_n ) //Копирование состояния до изменения.
- Set_event Preprocessing(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G,~i,~\omega_n} )
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \forall ~(s_{j},~\theta ,~\varphi )\in }
Set_event
- Ray Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Луч().Создать(, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \theta ,~\varphi ,~\omega _{n}} )
- Trace(Ray, G, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E_{end} )
- Postprocessing(G.Множество контрольных точек())
- SAcheck Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow SucApprox(G.Множество контрольных точек(), Pre_SCP, )
- Если SAcheck
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): i \leftarrow i+1
- Переход на 1.2
- ВЫХОД
[Таблица событий] Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Preprocessing(Геометрическая модель, Номер итерации, Частота)
Функция создает таблицу событий, необходимых обработать. В качестве событий - испускаемые моделью лучи на данной частоте.
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle T\leftarrow } Пустой односвязный список значений Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)} .
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle G\leftarrow } Геометрическая модель.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i \leftarrow} Номер итерации
- Частота
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ s_j \in
G.Множество первичных источников()
- Если .Антенна().Тип антенны().Амплитудно-частотная характеристика() Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \neq 0}
- Пока
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\varphi} \leftarrow 0
- Пока Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \varphi<2\pi
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0}
- .ДобавитьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \varphi \leftarrow \varphi +{\frac {\Delta _{\varphi }(s_{j},~\theta ,~\varphi )}{2^{i}}}}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \zeta_{\varphi} \leftarrow \zeta_{\varphi}+1
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta \leftarrow \theta + \frac{\Delta_{\theta} (s_j,~\theta)}{2^i}}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \zeta_{\theta} \leftarrow \zeta_{\theta}+1
- Если .Антенна().Тип антенны().Амплитудно-частотная характеристика() Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \neq 0}
- Вернуть Массив(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T )
Если Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \Delta _{\varphi }(s_{j},~\theta ,~\varphi )={\rm {const}}} , и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta_{\theta} (s_j,~\theta) = {\rm const}} , то есть углы распределены равномерно, таблица может быть реализована в виде массива значений Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle (s_{j},~\theta ,~\varphi )} , элементы которого могут заполняться параллельно, без синхронизации. Если же размер таблицы заранее не определен (общий случай), то таблица реализуется связанным списком, добавление элементов в который должно защищаться мьютексом на шаге 4.1.3.1.3.1.1, а алгоритм на заключительном шаге преобразует связанный список в массив с произвольным доступом. Второй путь при параллельном выполнении - создавать таблицы в локальной памяти потока, после выполнения которых - объединять таблицы в массив в основном потоке.
Параллельная форма
Параллельное выполнение в общем случае возможно только цикла, перебирающего первичные источники (шаг 4), так как распределение углов заранее не определено.
Пусть Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle P>0} - число потоков, выполняющих функцию. Пусть Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle T'} - массив изначально пустых связанных списков троек Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle (s_{j},~\theta ,~\varphi )} , так, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle T'_{i}} - -тый список массива, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 0\le i<P} .
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle i\leftarrow } Номер итерации
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega \leftarrow Частота
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle T'\leftarrow } Создать массив.
- G.Множество первичных источников()
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle t\leftarrow } индекс потока.
- Если .Антенна().Тип антенны().Амплитудно-частотная характеристика(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega
) Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \neq 0}
- Пока
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi \leftarrow 0
- Пока Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi<2\pi
- Если Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle i=0\vee \zeta _{\theta }{\bmod {2}}\neq 0\vee \zeta _{\varphi }{\bmod {2}}\neq 0}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle T'_{t}} .ДобавитьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \varphi \leftarrow \varphi +{\frac {\Delta _{\varphi }(s_{j},~\theta ,~\varphi )}{2^{i}}}}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\varphi} \leftarrow \zeta_{\varphi}+1
- Если Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle i=0\vee \zeta _{\theta }{\bmod {2}}\neq 0\vee \zeta _{\varphi }{\bmod {2}}\neq 0}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \theta \leftarrow \theta +{\frac {\Delta _{\theta }(s_{j},~\theta )}{2^{i}}}}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \zeta_{\theta} \leftarrow \zeta_{\theta}+1
- Вернуть МассивНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left(\bigsqcup_{t=0}^{P-1}T'_t\right)}
Trace
Функция трассирует луч через геометрическую модель и и фиксирует его прохождение вблизи контрольной точки.
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): R\leftarrow \infty
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): T\leftarrow NaN
- G.Множество отражающих объектов()
- .Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p \leftarrow Ray.Пересечение(.Плоскость())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn}
.Принадлежность()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r\leftarrow Ray.Пробег()
- Если
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R \leftarrow r
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T \leftarrow t_{mn}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): P \leftarrow p
- .Множество отражающих поверхностей()
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \forall ~ O_k \in
G.Множество плоскостей вывода результатов()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p \leftarrow Ray.Пересечение(Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): O_k .Плоскость())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): O_k
.Принадлежность()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r\leftarrow Ray.Пробег()
- Если
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): O_k .Ближайшая контрольная точка()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho .Зарегистрировать(Ray, , G.Среда распространения())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T \not\equiv
NaN
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \gamma \leftarrow Ray.Угол пересечения(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T .Плоскость())
- Ray.Отразить(Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): T,~P,~R,~\gamma , G.Среда распространения())
- Если Ray.Напряженность Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): >E_{end}
- Trace(Ray, G, )
Postprocessing
Функция "проявляет" поле в контрольных точках по накопленным значениям напряженности от всех пришедших лучей.
SucApprox
Функция сравнивает текущие результаты моделирования с результатами, полученными на предыдущем шаге. На выходе получаем флаг, по которому решаем, следует ли продолжать уточнять модель.
Свойства алгоритма
Сложность
Возможности распараллеливания
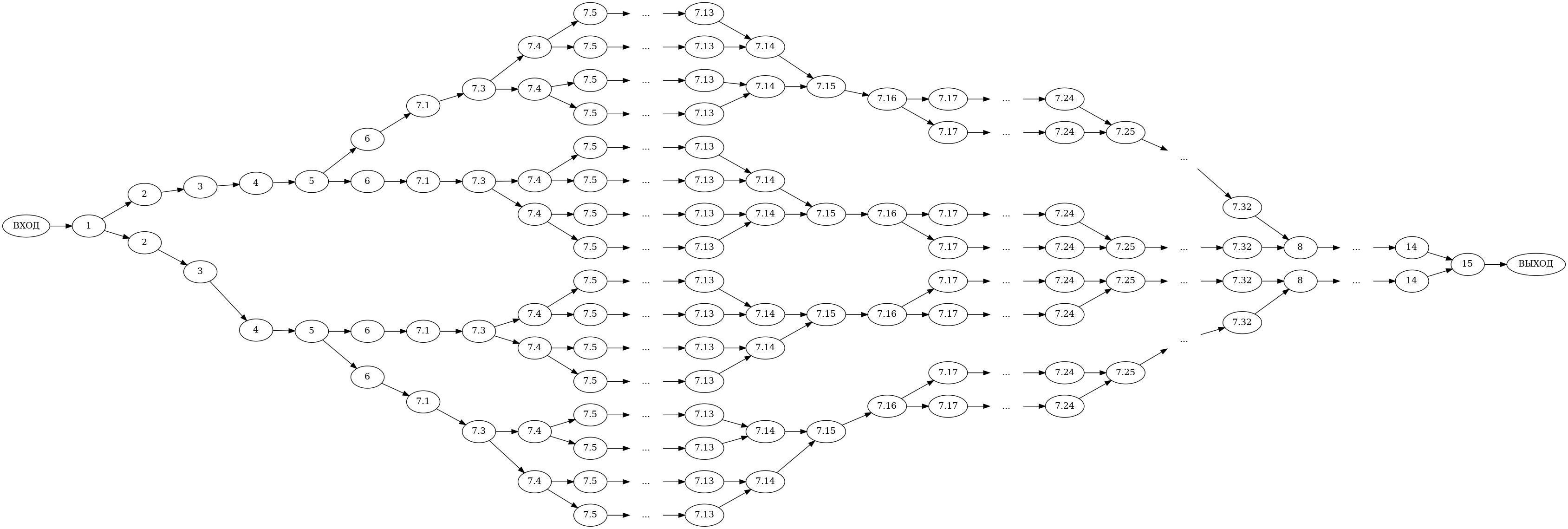
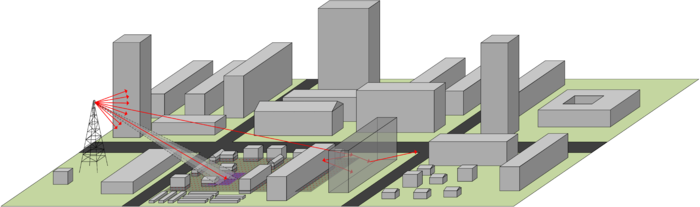
 , где
, где
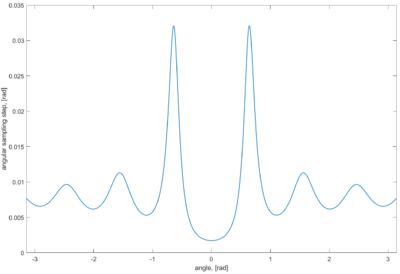
 - частота излучения;
- частота излучения; пересчитывается в соответствии с формулой:
пересчитывается в соответствии с формулой:
 , где
, где
 - расстояние до точки с высотой Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): h(x,y)
.
- расстояние до точки с высотой Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): h(x,y)
.
 , Distance,
, Distance, 
 .
. - входное описание среды распространения моделируемого поля, заданное
- входное описание среды распространения моделируемого поля, заданное 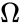 - список частот, на которых необходимо провести моделирование.
- список частот, на которых необходимо провести моделирование. - критерий разности между текущим и предыдущим результатом моделирования, при которой можно считать, что поле промоделированно точно.
- критерий разности между текущим и предыдущим результатом моделирования, при которой можно считать, что поле промоделированно точно.
 Preprocessing(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G,~i,~\omega_n}
)
Preprocessing(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G,~i,~\omega_n}
) )
) Частота
Частота )
)



 .ДобавитьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)}
.ДобавитьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)}
 -тый список массива, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 0\le i<P}
.
-тый список массива, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 0\le i<P}
.



 .Множество отражающих поверхностей()
.Множество отражающих поверхностей()

 )
)


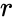 ,
,  )
)