Распространение радиоволн ВЧ/Напряженность: различия между версиями
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 8: | Строка 8: | ||
В результате распространения излученного элемента волны на расстояние <math>r_1</math> напряженность поля падает в <math>r_1 e^{ikr_1}</math> раз, становясь равной | В результате распространения излученного элемента волны на расстояние <math>r_1</math> напряженность поля падает в <math>r_1 e^{ikr_1}</math> раз, становясь равной | ||
:<math>\vec{\dot E}\left(r_1\right)=\vec{\dot E_0}r_0 y_1 = \vec{\dot E_0}\frac{r_0}{r_1}e^{-ikr_1}</math>, где: | :<math>\vec{\dot E}\left(r_1\right)=\vec{\dot E_0}r_0 y_1 \left(r_1\right) = \vec{\dot E_0}\frac{r_0}{r_1}e^{-ikr_1}</math>, где: | ||
* <math>y_1 | * <math>y_1 \left(r_1\right) = \frac{1}{r_1}e^{-ikr_1}</math> - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны, | ||
* <math>\dot k = \omega \sqrt{\dot \varepsilon \dot \mu}</math> - комплексное волновое число | * <math>\dot k = \omega \sqrt{\dot \varepsilon \dot \mu}</math> - комплексное волновое число | ||
** <math>\dot \varepsilon = \varepsilon' - i \varepsilon''</math> | ** <math>\dot \varepsilon = \varepsilon' - i \varepsilon''</math> | ||
| Строка 26: | Строка 26: | ||
Тогда, в результате распространения волнового элемента на расстояние <math>r_1 + r_2</math> от источника в одной и той же изотропной среде, результирующая напряженность станет равной | Тогда, в результате распространения волнового элемента на расстояние <math>r_1 + r_2</math> от источника в одной и той же изотропной среде, результирующая напряженность станет равной | ||
:<math>\vec{\dot E}\left(r_1 | :<math>\vec{\dot E}\left(r_1, r_2\right) = \vec{\dot E_0}r_0 y\left(r_1, r_2\right)=\vec{\dot E_0}r_0 y_1\left(r_1, r_2\right)\left(r_1, r_2\right)y_2\left(r_1, r_2\right)</math>, | ||
где <math> | где <math>y_1\left(r_1, r_2\right) = \left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{1}{2}}\frac{e^{-ikr_1}}{r_1}</math>, <math>y'_2\left(r_1, r_2\right) = \left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{1}{2}}\frac{e^{-ikr_2}}{r_2}</math> и <math>y\left(r_1, r_2\right) = y_1\left(r_1, r_2\right)y_2\left(r_1, r_2\right)=\left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{2}{2}}\frac{e^{-ikr_1}e^{-ikr_2}}{r_1 r_2} = \frac{e^{-ik\left(r_1 + r_2\right)}}{r_1 + r_2}</math>. | ||
В более общем случае | |||
:<math>\vec{\dot E}\left(r_1, \dots, r_n\right) = \vec{\dot E_0}r_0 y\left(r_1, \dots, r_n\right)=\vec{\dot E_0}r_0\prod_{j=1}^{n}y_j\left(r_1, \dots, r_n\right)= | |||
:<math>\vec{\dot E}\left(\ | \vec{\dot E_0}\frac{r_0}{\sum_{i=1}^{n} r_i}e^{-i\left(\sum_{i=1}^{n} k_i r_i\right)}</math>, | ||
где <math>y_j\left(r_1, \dots, r_n\right) = \left(\frac{\prod_{j'=1}^{n}r_{j'}}{\sum_{j'=1}^{n}r_{j'}}\right)^\frac{1}{n}\frac{e^{-ik_jr_j}}{r_j}</math>. | |||
=Модель отражения= | =Модель отражения= | ||
Пусть электрическая напряженность волнового элемента, падающего на плоскую поверхность с нормалью <math>\vec{n}</math>, задается некоторым комплексным вектором <math>\vec{\dot | Пусть электрическая напряженность волнового элемента, падающего на плоскую поверхность с нормалью <math>\vec{n}</math>, задается некоторым комплексным вектором <math>\vec{\dot E}_\mathrm{inc}</math>. Пусть эта поверхность является границей раздела двух сред. | ||
* среды с четверкой параметров <math>\left \{ \dot \varepsilon_1,~\dot \mu_1,~\dot k_1,~\dot Z_1 \right \}</math>, в которой распространяется падающая волна, и | |||
* среды с четверкой параметров <math>\left \{ \dot \varepsilon_2,~\dot \mu_1,~\dot k_2,~\dot Z_2 \right \}</math>, на границу которой падает волна. | |||
Соответственно, <math>\varphi_1</math> - угол падения (и отражения), а угол <math>\varphi_2</math> - угол преломления. | |||
[[Файл:Ref Norm Pol.png|400px|thumb|right|Перпендикулярная поляризация]] | [[Файл:Ref Norm Pol.png|400px|thumb|right|Перпендикулярная поляризация]] | ||
| Строка 54: | Строка 56: | ||
** <math>\beta</math> - угол магнитных потерь; | ** <math>\beta</math> - угол магнитных потерь; | ||
* <math>\dot k = \omega \sqrt{\dot \varepsilon \dot \mu}</math> - комплексное волновое число; | * <math>\dot k = \omega \sqrt{\dot \varepsilon \dot \mu}</math> - комплексное волновое число; | ||
* <math>\dot | * <math>\dot Z = \sqrt{\frac{\dot \mu}{\dot \varepsilon}}</math> - комплексное волновое сопротивление; | ||
* <math>n_1\sin\varphi_1=n_2\sin\varphi_2</math> согласно [https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%A1%D0%BD%D0%B5%D0%BB%D0%BB%D0%B8%D1%83%D1%81%D0%B0 закону Снеллиуса], причем | |||
** <math>n=\frac{k}{\omega}=\sqrt{\mu\varepsilon}</math> - коэффициент преломления соответствующей среды. | |||
Тогда коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля): | Тогда коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля) соответственно: | ||
<math>\ | :<math> | ||
\rho_\mathrm{s} = \frac{Z_2 \cos \varphi_1 - Z_1 \cos \varphi_2}{Z_2 \cos \varphi_2 + Z_1 \cos \varphi_1}, | |||
</math> | |||
:<math> | |||
\rho_\mathrm{p} = \frac{Z_2 \cos \varphi_2 - Z_1 \cos \varphi_1}{Z_2 \cos \varphi_1 + Z_1 \cos \varphi_2}, | |||
</math> | |||
<math>\ | Если направляющий вектор <math>\vec{v}</math> луча '''параллелен''' нормали к отражающей поверхности, для расчета отраженной волны необходимо и достаточно аддитивно обратить вектор электрической напряженности <math>\vec{\dot E}_\mathrm{inc}</math> падающей на поверхность волны и умножить этот вектор на скаляр, получаемый из приведенных выше формул Френеля для случая <math>\varphi_1 = \varphi_2 = 0</math>, т.е. | ||
:<math>\vec{\dot E}_\mathrm{refl} = Y_\mathrm{refl}\vec{\dot E}_\mathrm{inc} = \begin{bmatrix} | |||
<math>\vec {\dot | -\rho & 0 & 0 \\ | ||
0 & -\rho & 0 \\ | |||
0 & 0 & -\rho | |||
\end{bmatrix}</math>, | |||
где <math>\rho=\frac{Z_2-Z_1}{Z_2+Z_1}</math>. | |||
''То есть для случая нормального падения на отражающую поверхность'' | |||
<math>\ | :<math>Y_\mathrm{refl} = \begin{bmatrix} | ||
-\rho & 0 & 0 \\ | |||
0 & -\rho & 0 \\ | |||
0 & 0 & -\rho | |||
\end{bmatrix}</math>. | |||
Рассмотрим случай, когда направляющий вектор <math>\vec{v}</math> луча '''не параллелен''' нормали к отражающей поверхности. | |||
<math> | Пусть <math>\vec{\dot E'}_\mathrm{inc} = T_\mathrm{inc}\vec{\dot E}_\mathrm{inc}</math> - вектор электрической напряженности падающей на поверхность волны. Вектор <math>\vec{\dot E'}_\mathrm{inc}</math> выражен в базисе <math>\langle\vec{e_0},\vec{e_1},\vec{e_2}\rangle</math>, заданном так, что <math>\vec{e_0}</math> определяет направление, перпендикулярное плоскости падения волны, т.е. плоскости, которой принадлежат нормаль <math>\vec{n}</math> к отражающей поверхности и направляющий вектор <math>\vec{v}</math> луча; вектор <math>\vec{e_1}</math> задает направление, перпендикулярное <math>\vec{e_0}</math> и одновременно перпендикулярное <math>\vec{v}</math>; а вектор <math>\vec{e_2}</math> сонаправлен <math>\vec{v}</math>. Тогда выраженный в таком базисе вектор электрической напряженности, <math>\vec{\dot E'}_\mathrm{inc}</math>, будет иметь три компоненты, первая из которых задает перпендикулярно поляризованную часть напряженности <math>\vec{\dot E}_\mathrm{inc}</math>, вторая - параллельно поляризованную часть, а третья компонента вектора <math>\vec{\dot E'}_\mathrm{inc}</math> будет равна нулю как компонента, параллельная вектору Пойнтинга. Поэтому для расчета электрической напряженности отраженной волны достаточно умножить первую компоненту <math>\vec{\dot E'}_\mathrm{inc}</math> на <math>\rho_\mathrm{s}</math>, вторую компоненту - на <math>\rho_\mathrm{p}</math>, а третью - проигнорировать (или умножить имеющийся в ней ноль на произвольное значение). | ||
Тогда <math>\vec{\dot E}_\mathrm{inc} = \begin{bmatrix}\vec{e_0} & \vec{e_1} & \vec{e_2}\end{bmatrix}\vec{\dot E'}_\mathrm{inc}</math>, поэтому <math>T_\mathrm{inc}=\begin{bmatrix}\vec{e_0} & \vec{e_1} & \vec{e_2}\end{bmatrix}^{-1}</math>. | |||
<math> | При этом вектора базиса можно расчитать, как указано выше, с помощью векторного произведения: | ||
:<math>\vec{e_0}=\vec{v}\times\vec{n}</math>; | |||
:<math>\vec{e_1}=\vec{v}\times\left(\vec{v}\times\vec{n}\right)</math>; | |||
:<math>\vec{e_2}=\vec{v}</math>. | |||
Как указано выше, базис <math>\langle\vec{e_0},\vec{e_1},\vec{e_2}\rangle</math> ортогонален, поэтому матрица <math>T_\mathrm{inc}</math> также является ортогональной, и поэтому <math>T_\mathrm{inc}^{-1}=T_\mathrm{inc}^T</math>. | |||
Тогда вектор напряженности отраженной волны, в мировых координатах, равен | |||
:<math>\vec{\dot E}_\mathrm{refl} = Y_\mathrm{refl}\vec{E}_\mathrm{inc} = T_\mathrm{inc}^{-1}T_\mathrm{refl}T_\mathrm{inc}\vec{\dot E}_\mathrm{inc} = | |||
\begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix} | |||
\begin{bmatrix} | |||
1 & 0 & 0 \\ | |||
0 & \cos(\pi - 2 \varphi_1) & \sin(\pi - 2 \varphi_1) \\ | |||
0 & -\sin(\pi - 2 \varphi_1) & \cos(\pi - 2 \varphi_1) | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
\rho_\mathrm{s} & 0 & 0 \\ | |||
0 & \rho_\mathrm{p} & 0 \\ | |||
0 & 0 & 1 | |||
\end{bmatrix} | |||
\begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix}^T</math>. | |||
''То есть, если падение волны не нормально плоскости отражающей поверхности, то,'' после упрощения, | |||
:<math>Y_\mathrm{refl} = | |||
:<math>\ | \begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix} | ||
\begin{bmatrix} | |||
\rho_\mathrm{s} & 0 & 0 \\ | |||
0 & -\rho_\mathrm{p}\cos 2 \varphi_1 & \sin 2 \varphi_1 \\ | |||
0 & -\rho_\mathrm{p}\sin 2 \varphi_1 & -\cos 2 \varphi_1 | |||
\end{bmatrix} | |||
\begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix}^T</math>. | |||
<math> | ''Таким образом, напряженность электрического поля волнового элемента в результате его <math>m</math> отражений и <math>m + 1</math> прохождений в (различных изотропных) средах рассчитывается по формуле'' | ||
:<math>\vec{E} = y_{m+1} \left(\prod_{j=1}^m Y_j y_j\right) \vec{E}_0 r_0 = \prod_{j=1}^{m} Y_j \cdot \prod_{j=1}^{m + 1} y_j \cdot \vec{E}_0 r_0 = \prod_{j=1}^{m} Y_j \cdot \frac{e^{-i\sum_{j=1}^{m+1} k_j r_j}}{\sum_{j=1}^{m+1} r_j}</math>. | |||
:<math>\ | |||
=Метод реализации= | |||
Напряженность поля - реализуется трехкомпонентным комплексным вектором <math>\vec{\dot E}=\begin{pmatrix}\dot E_x & \dot E_y & \dot E_z\end{pmatrix}^T</math>. | |||
<math>\ | Состояние объекта, реализующего волновой элемент, задается: | ||
* <math>\vec{\varphi}_0 = \vec{\dot E}_0 r_0</math>, где <math>r_0</math> - расстояние в дальней зоне источника, на котором снято значение напряженности <math>\vec{\dot E}_0</math>[[Распространение_радиоволн_ВЧ/Первичный источник|первичного источника]]; | |||
* <math>\omega</math> - круговая частота волнового элемента; | |||
* <math>r_{\sum} = \sum_{j=0}^m r_j</math> - расстояние, пройденное в общем волновым элементом от первичного источника до его текущего расположения; | |||
* <math>\varphi_{\sum} = \sum_{j=0}^m k_j r_j</math> - фазовый сдвиг, которому подвергся волновой элемент в результате прохождения им расстояния <math>r_{\sum}</math>; | |||
* <math>Y_{\prod}=\prod_{j=1}^n Y_j</math> - матрица, реализующая отражение вектора напряженности. | |||
<math> | Тогда напряженность волнового элемента после всех распространений и отражений будет | ||
:<math>E=Y_{\prod}\frac{e^{-i\varphi_{\sum}}}{r_{\sum}}</math>. | |||
==Методы== | |||
* <tt>Изменить по пробегу(Пробег, Комплексное волновое число)</tt> | |||
* <tt>Изменить по отражению(КДП_1*, КМП_1**, КДП_2, КМП_2, Вектор(Направление луча), Вектор(Нормаль грани))</tt>=== | |||
<tt>*</tt> - комплексная диэлектрическая проницаемость, | |||
<tt>**</tt> - комплексная магнитная проницаемость. | |||
< | |||
< | |||
Текущая версия на 03:28, 13 октября 2018
Трехкомпонентный комплексный вектор который задается волновым элементом, порождаемым источником , в результате распространения и отражений в среде.
Вектор рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
Модель распространения
Пусть - дальняя зона, расстояние, на котором для источника снята начальная напряженность .
В результате распространения излученного элемента волны на расстояние напряженность поля падает в раз, становясь равной
- , где:
- - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны,
- - комплексное волновое число
Таким образом .
Здесь первая экспонента является коэффициентом поглощения среды на расстоянии , а
- погонным затуханием среды [дБ/м]
В частности, при отсутствии инерционности поляризации и намагничивания :
.
Тогда, в результате распространения волнового элемента на расстояние от источника в одной и той же изотропной среде, результирующая напряженность станет равной
- ,
где , и .
В более общем случае
- ,
где .
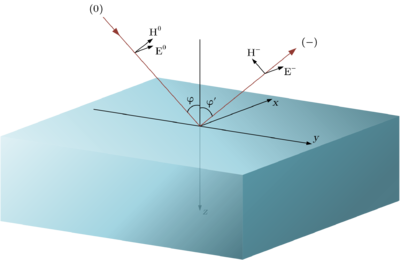
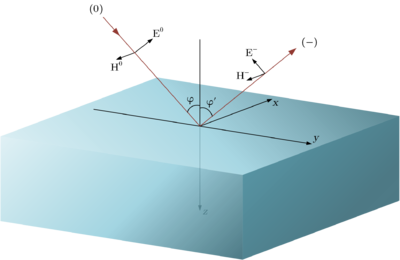
Модель отражения
Пусть электрическая напряженность волнового элемента, падающего на плоскую поверхность с нормалью , задается некоторым комплексным вектором . Пусть эта поверхность является границей раздела двух сред.
- среды с четверкой параметров , в которой распространяется падающая волна, и
- среды с четверкой параметров , на границу которой падает волна.
Соответственно, - угол падения (и отражения), а угол - угол преломления.
Здесь:
- - комплексная диэлектрическая проницаемость, где
- - диэлектрическая проницаемость среды,
- - проводимость среды,
- - круговая частота волны,
- - угол диэлектрических потерь;
- - комплексная магнитная проницаемость, где
- - магнитная проницаемость среды,
- - угол магнитных потерь;
- - комплексное волновое число;
- - комплексное волновое сопротивление;
- согласно закону Снеллиуса, причем
- - коэффициент преломления соответствующей среды.
Тогда коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля) соответственно:
Если направляющий вектор луча параллелен нормали к отражающей поверхности, для расчета отраженной волны необходимо и достаточно аддитивно обратить вектор электрической напряженности падающей на поверхность волны и умножить этот вектор на скаляр, получаемый из приведенных выше формул Френеля для случая , т.е.
- ,
где .
То есть для случая нормального падения на отражающую поверхность
- .
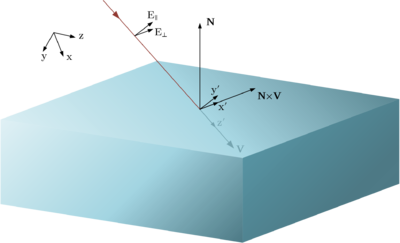
Рассмотрим случай, когда направляющий вектор луча не параллелен нормали к отражающей поверхности.
Пусть - вектор электрической напряженности падающей на поверхность волны. Вектор выражен в базисе , заданном так, что определяет направление, перпендикулярное плоскости падения волны, т.е. плоскости, которой принадлежат нормаль к отражающей поверхности и направляющий вектор луча; вектор задает направление, перпендикулярное и одновременно перпендикулярное ; а вектор сонаправлен . Тогда выраженный в таком базисе вектор электрической напряженности, , будет иметь три компоненты, первая из которых задает перпендикулярно поляризованную часть напряженности , вторая - параллельно поляризованную часть, а третья компонента вектора будет равна нулю как компонента, параллельная вектору Пойнтинга. Поэтому для расчета электрической напряженности отраженной волны достаточно умножить первую компоненту на , вторую компоненту - на , а третью - проигнорировать (или умножить имеющийся в ней ноль на произвольное значение).
Тогда , поэтому .
При этом вектора базиса можно расчитать, как указано выше, с помощью векторного произведения:
- ;
- ;
- .
Как указано выше, базис ортогонален, поэтому матрица также является ортогональной, и поэтому .
Тогда вектор напряженности отраженной волны, в мировых координатах, равен
- .
То есть, если падение волны не нормально плоскости отражающей поверхности, то, после упрощения,
- .
Таким образом, напряженность электрического поля волнового элемента в результате его отражений и прохождений в (различных изотропных) средах рассчитывается по формуле
- .
Метод реализации
Напряженность поля - реализуется трехкомпонентным комплексным вектором .
Состояние объекта, реализующего волновой элемент, задается:
- , где - расстояние в дальней зоне источника, на котором снято значение напряженности первичного источника;
- - круговая частота волнового элемента;
- - расстояние, пройденное в общем волновым элементом от первичного источника до его текущего расположения;
- - фазовый сдвиг, которому подвергся волновой элемент в результате прохождения им расстояния ;
- - матрица, реализующая отражение вектора напряженности.
Тогда напряженность волнового элемента после всех распространений и отражений будет
- .
Методы
- Изменить по пробегу(Пробег, Комплексное волновое число)
- Изменить по отражению(КДП_1*, КМП_1**, КДП_2, КМП_2, Вектор(Направление луча), Вектор(Нормаль грани))===
* - комплексная диэлектрическая проницаемость, ** - комплексная магнитная проницаемость.
 который задается волновым элементом, порождаемым
который задается волновым элементом, порождаемым  , в результате распространения и отражений в среде.
, в результате распространения и отражений в среде.
 рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
 - дальняя зона, расстояние, на котором для источника
- дальняя зона, расстояние, на котором для источника  .
.
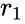 напряженность поля падает в
напряженность поля падает в  раз, становясь равной
раз, становясь равной
 , где:
, где: - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны,
- скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны, - комплексное волновое число
- комплексное волновое число



 .
.
 - погонным затуханием среды [дБ/м]
- погонным затуханием среды [дБ/м]
 :
:
 .
.
 от источника в одной и той же изотропной среде, результирующая напряженность станет равной
от источника в одной и той же изотропной среде, результирующая напряженность станет равной
 ,
, ,
,  и
и  .
.
 ,
, .
.
 , задается некоторым комплексным вектором
, задается некоторым комплексным вектором  . Пусть эта поверхность является границей раздела двух сред.
. Пусть эта поверхность является границей раздела двух сред.
 , в которой распространяется падающая волна, и
, в которой распространяется падающая волна, и , на границу которой падает волна.
, на границу которой падает волна. - угол падения (и отражения), а угол
- угол падения (и отражения), а угол  - угол преломления.
- угол преломления.
 - комплексная диэлектрическая проницаемость, где
- комплексная диэлектрическая проницаемость, где
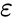 - диэлектрическая проницаемость среды,
- диэлектрическая проницаемость среды, - проводимость среды,
- проводимость среды, - круговая частота волны,
- круговая частота волны, - угол диэлектрических потерь;
- угол диэлектрических потерь; - комплексная магнитная проницаемость, где
- комплексная магнитная проницаемость, где
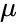 - магнитная проницаемость среды,
- магнитная проницаемость среды, - угол магнитных потерь;
- угол магнитных потерь; - комплексное волновое сопротивление;
- комплексное волновое сопротивление; согласно
согласно  - коэффициент преломления соответствующей среды.
- коэффициент преломления соответствующей среды.

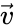 луча параллелен нормали к отражающей поверхности, для расчета отраженной волны необходимо и достаточно аддитивно обратить вектор электрической напряженности
луча параллелен нормали к отражающей поверхности, для расчета отраженной волны необходимо и достаточно аддитивно обратить вектор электрической напряженности  , т.е.
, т.е.
 ,
, .
.
 .
. - вектор электрической напряженности падающей на поверхность волны. Вектор
- вектор электрической напряженности падающей на поверхность волны. Вектор  выражен в базисе
выражен в базисе  , заданном так, что
, заданном так, что  определяет направление, перпендикулярное плоскости падения волны, т.е. плоскости, которой принадлежат нормаль
определяет направление, перпендикулярное плоскости падения волны, т.е. плоскости, которой принадлежат нормаль  задает направление, перпендикулярное
задает направление, перпендикулярное  сонаправлен
сонаправлен  , вторую компоненту - на
, вторую компоненту - на  , а третью - проигнорировать (или умножить имеющийся в ней ноль на произвольное значение).
, а третью - проигнорировать (или умножить имеющийся в ней ноль на произвольное значение).
 , поэтому
, поэтому  .
.
 ;
; ;
; .
. также является ортогональной, и поэтому
также является ортогональной, и поэтому  .
.
 .
. .
. отражений и
отражений и  прохождений в (различных изотропных) средах рассчитывается по формуле
прохождений в (различных изотропных) средах рассчитывается по формуле
 .
. .
.
 , где
, где 
 - расстояние, пройденное в общем волновым элементом от первичного источника до его текущего расположения;
- расстояние, пройденное в общем волновым элементом от первичного источника до его текущего расположения; - фазовый сдвиг, которому подвергся волновой элемент в результате прохождения им расстояния
- фазовый сдвиг, которому подвергся волновой элемент в результате прохождения им расстояния  ;
; - матрица, реализующая отражение вектора напряженности.
- матрица, реализующая отражение вектора напряженности. .
.