Распространение радиоволн ВЧ/Напряженность: различия между версиями
Nigiluk (обсуждение | вклад) |
|||
| (не показано 14 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
Трехкомпонентный комплексный вектор <math> \vec{\dot E} =\begin{pmatrix} \dot E_{x} \\ \dot E_{y} \\ \dot E_{z}\end{pmatrix}</math> | Трехкомпонентный комплексный вектор <math> \vec{\dot E} =\begin{pmatrix} \dot E_{x} \\ \dot E_{y} \\ \dot E_{z}\end{pmatrix},</math> который задается волновым элементом, порождаемым [[Распространение радиоволн ВЧ/Первичный источник|источником]] <math>S</math>, в результате распространения и отражений в среде. | ||
= | |||
==< | Вектор <math>\vec{\dot E}</math> рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом. | ||
=Модель распространения= | |||
Пусть <math>r_0</math> - дальняя зона, расстояние, на котором для источника <math>S</math> снята начальная напряженность <math>\vec{\dot E_0}</math>. | |||
В результате распространения излученного элемента волны на расстояние <math>r_1</math> напряженность поля падает в <math>r_1 e^{ikr_1}</math> раз, становясь равной | |||
:<math>\vec{\dot E}\left(r_1\right)=\vec{\dot E_0}r_0 y_1 \left(r_1\right) = \vec{\dot E_0}\frac{r_0}{r_1}e^{-ikr_1}</math>, где: | |||
* <math>y_1 \left(r_1\right) = \frac{1}{r_1}e^{-ikr_1}</math> - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны, | |||
* <math>\dot k = \omega \sqrt{\dot \varepsilon \dot \mu}</math> - комплексное волновое число | |||
** <math>\dot \varepsilon = \varepsilon' - i \varepsilon''</math> | |||
** <math>\dot \mu= \mu' - i \mu''</math> | |||
** <math>\dot k= k' - i k''</math> | |||
Таким образом <math>\vec{\dot E}\left(r_1\right) = \vec{\dot E_0} \frac{r_0}{r_1}e^{-k''r_1}e^{-ik'r_1}</math>. | |||
Здесь первая экспонента является коэффициентом поглощения среды на расстоянии <math>r_1</math>, а | |||
<math>L = k''20 \lg e</math> - погонным затуханием среды [дБ/м] | |||
В частности, при отсутствии инерционности поляризации и намагничивания <math>\alpha = 0,~\beta=0</math> : | |||
<math>k'=k=\omega \sqrt{\varepsilon \mu},~k''=\frac {\sigma}{2} \sqrt \frac {\mu}{\varepsilon}</math>. | |||
Тогда, в результате распространения волнового элемента на расстояние <math>r_1 + r_2</math> от источника в одной и той же изотропной среде, результирующая напряженность станет равной | |||
:<math>\vec{\dot E}\left(r_1, r_2\right) = \vec{\dot E_0}r_0 y\left(r_1, r_2\right)=\vec{\dot E_0}r_0 y_1\left(r_1, r_2\right)\left(r_1, r_2\right)y_2\left(r_1, r_2\right)</math>, | |||
где <math>y_1\left(r_1, r_2\right) = \left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{1}{2}}\frac{e^{-ikr_1}}{r_1}</math>, <math>y'_2\left(r_1, r_2\right) = \left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{1}{2}}\frac{e^{-ikr_2}}{r_2}</math> и <math>y\left(r_1, r_2\right) = y_1\left(r_1, r_2\right)y_2\left(r_1, r_2\right)=\left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{2}{2}}\frac{e^{-ikr_1}e^{-ikr_2}}{r_1 r_2} = \frac{e^{-ik\left(r_1 + r_2\right)}}{r_1 + r_2}</math>. | |||
В более общем случае | |||
:<math>\vec{\dot E}\left(r_1, \dots, r_n\right) = \vec{\dot E_0}r_0 y\left(r_1, \dots, r_n\right)=\vec{\dot E_0}r_0\prod_{j=1}^{n}y_j\left(r_1, \dots, r_n\right)= | |||
\vec{\dot E_0}\frac{r_0}{\sum_{i=1}^{n} r_i}e^{-i\left(\sum_{i=1}^{n} k_i r_i\right)}</math>, | |||
где <math>y_j\left(r_1, \dots, r_n\right) = \left(\frac{\prod_{j'=1}^{n}r_{j'}}{\sum_{j'=1}^{n}r_{j'}}\right)^\frac{1}{n}\frac{e^{-ik_jr_j}}{r_j}</math>. | |||
=Модель отражения= | |||
Пусть электрическая напряженность волнового элемента, падающего на плоскую поверхность с нормалью <math>\vec{n}</math>, задается некоторым комплексным вектором <math>\vec{\dot E}_\mathrm{inc}</math>. Пусть эта поверхность является границей раздела двух сред. | |||
* среды с четверкой параметров <math>\left \{ \dot \varepsilon_1,~\dot \mu_1,~\dot k_1,~\dot Z_1 \right \}</math>, в которой распространяется падающая волна, и | |||
* среды с четверкой параметров <math>\left \{ \dot \varepsilon_2,~\dot \mu_1,~\dot k_2,~\dot Z_2 \right \}</math>, на границу которой падает волна. | |||
Соответственно, <math>\varphi_1</math> - угол падения (и отражения), а угол <math>\varphi_2</math> - угол преломления. | |||
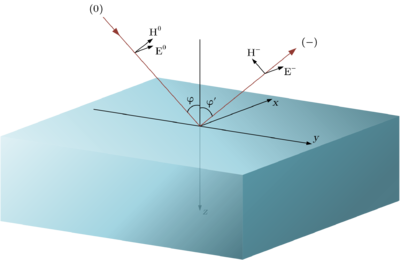
[[Файл:Ref Norm Pol.png|400px|thumb|right|Перпендикулярная поляризация]] | [[Файл:Ref Norm Pol.png|400px|thumb|right|Перпендикулярная поляризация]] | ||
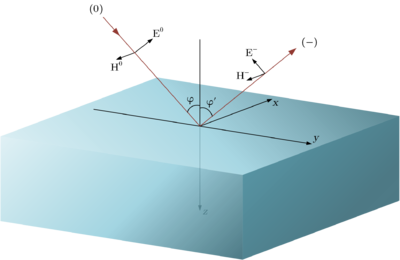
[[Файл:Ref Parall Pol.png|400px|thumb|right|Параллельная поляризация]] | [[Файл:Ref Parall Pol.png|400px|thumb|right|Параллельная поляризация]] | ||
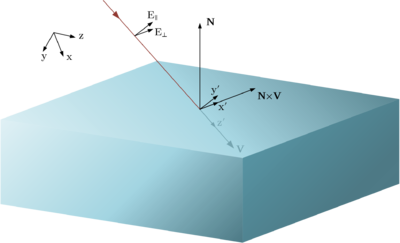
[[Файл:Ref_Rot_Axes.png|400px|thumb|right|Поворот координатных осей]] | |||
:<math>\ | |||
Здесь: | |||
* <math>\dot \varepsilon = \varepsilon \cos \alpha - i ( \frac{\sigma}{\omega} + \varepsilon \sin \alpha)</math> - комплексная диэлектрическая проницаемость, где | |||
** <math>\varepsilon</math> - диэлектрическая проницаемость среды, | |||
** <math>\sigma</math> - проводимость среды, | |||
** <math>\omega</math> - круговая частота волны, | |||
** <math>\alpha</math> - угол диэлектрических потерь; | |||
* <math>\dot \mu = \mu \cos \beta - i \mu \sin \beta</math> - комплексная магнитная проницаемость, где | |||
** <math>\mu</math> - магнитная проницаемость среды, | |||
** <math>\beta</math> - угол магнитных потерь; | |||
* <math>\dot k = \omega \sqrt{\dot \varepsilon \dot \mu}</math> - комплексное волновое число; | |||
* <math>\dot Z = \sqrt{\frac{\dot \mu}{\dot \varepsilon}}</math> - комплексное волновое сопротивление; | |||
* <math>n_1\sin\varphi_1=n_2\sin\varphi_2</math> согласно [https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%A1%D0%BD%D0%B5%D0%BB%D0%BB%D0%B8%D1%83%D1%81%D0%B0 закону Снеллиуса], причем | |||
** <math>n=\frac{k}{\omega}=\sqrt{\mu\varepsilon}</math> - коэффициент преломления соответствующей среды. | |||
Тогда коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля) соответственно: | |||
:<math> | |||
\rho_\mathrm{s} = \frac{Z_2 \cos \varphi_1 - Z_1 \cos \varphi_2}{Z_2 \cos \varphi_2 + Z_1 \cos \varphi_1}, | |||
</math> | |||
:<math> | |||
\rho_\mathrm{p} = \frac{Z_2 \cos \varphi_2 - Z_1 \cos \varphi_1}{Z_2 \cos \varphi_1 + Z_1 \cos \varphi_2}, | |||
</math> | |||
Если направляющий вектор <math>\vec{v}</math> луча '''параллелен''' нормали к отражающей поверхности, для расчета отраженной волны необходимо и достаточно аддитивно обратить вектор электрической напряженности <math>\vec{\dot E}_\mathrm{inc}</math> падающей на поверхность волны и умножить этот вектор на скаляр, получаемый из приведенных выше формул Френеля для случая <math>\varphi_1 = \varphi_2 = 0</math>, т.е. | |||
:<math>\vec{\dot E}_\mathrm{refl} = Y_\mathrm{refl}\vec{\dot E}_\mathrm{inc} = \begin{bmatrix} | |||
-\rho & 0 & 0 \\ | |||
0 & -\rho & 0 \\ | |||
0 & 0 & -\rho | |||
\end{bmatrix}</math>, | |||
где <math>\rho=\frac{Z_2-Z_1}{Z_2+Z_1}</math>. | |||
''То есть для случая нормального падения на отражающую поверхность'' | |||
:<math>Y_\mathrm{refl} = \begin{bmatrix} | |||
-\rho & 0 & 0 \\ | |||
0 & -\rho & 0 \\ | |||
0 & 0 & -\rho | |||
\end{bmatrix}</math>. | |||
Рассмотрим случай, когда направляющий вектор <math>\vec{v}</math> луча '''не параллелен''' нормали к отражающей поверхности. | |||
Пусть <math>\vec{\dot E'}_\mathrm{inc} = T_\mathrm{inc}\vec{\dot E}_\mathrm{inc}</math> - вектор электрической напряженности падающей на поверхность волны. Вектор <math>\vec{\dot E'}_\mathrm{inc}</math> выражен в базисе <math>\langle\vec{e_0},\vec{e_1},\vec{e_2}\rangle</math>, заданном так, что <math>\vec{e_0}</math> определяет направление, перпендикулярное плоскости падения волны, т.е. плоскости, которой принадлежат нормаль <math>\vec{n}</math> к отражающей поверхности и направляющий вектор <math>\vec{v}</math> луча; вектор <math>\vec{e_1}</math> задает направление, перпендикулярное <math>\vec{e_0}</math> и одновременно перпендикулярное <math>\vec{v}</math>; а вектор <math>\vec{e_2}</math> сонаправлен <math>\vec{v}</math>. Тогда выраженный в таком базисе вектор электрической напряженности, <math>\vec{\dot E'}_\mathrm{inc}</math>, будет иметь три компоненты, первая из которых задает перпендикулярно поляризованную часть напряженности <math>\vec{\dot E}_\mathrm{inc}</math>, вторая - параллельно поляризованную часть, а третья компонента вектора <math>\vec{\dot E'}_\mathrm{inc}</math> будет равна нулю как компонента, параллельная вектору Пойнтинга. Поэтому для расчета электрической напряженности отраженной волны достаточно умножить первую компоненту <math>\vec{\dot E'}_\mathrm{inc}</math> на <math>\rho_\mathrm{s}</math>, вторую компоненту - на <math>\rho_\mathrm{p}</math>, а третью - проигнорировать (или умножить имеющийся в ней ноль на произвольное значение). | |||
Тогда <math>\vec{\dot E}_\mathrm{inc} = \begin{bmatrix}\vec{e_0} & \vec{e_1} & \vec{e_2}\end{bmatrix}\vec{\dot E'}_\mathrm{inc}</math>, поэтому <math>T_\mathrm{inc}=\begin{bmatrix}\vec{e_0} & \vec{e_1} & \vec{e_2}\end{bmatrix}^{-1}</math>. | |||
<math>\ | При этом вектора базиса можно расчитать, как указано выше, с помощью векторного произведения: | ||
:<math>\ | :<math>\vec{e_0}=\vec{v}\times\vec{n}</math>; | ||
:<math>\ | :<math>\vec{e_1}=\vec{v}\times\left(\vec{v}\times\vec{n}\right)</math>; | ||
:<math>\vec{e_2}=\vec{v}</math>. | |||
<math>\ | Как указано выше, базис <math>\langle\vec{e_0},\vec{e_1},\vec{e_2}\rangle</math> ортогонален, поэтому матрица <math>T_\mathrm{inc}</math> также является ортогональной, и поэтому <math>T_\mathrm{inc}^{-1}=T_\mathrm{inc}^T</math>. | ||
Тогда вектор напряженности отраженной волны, в мировых координатах, равен | |||
:<math>\vec{\dot E}_\mathrm{refl} = Y_\mathrm{refl}\vec{E}_\mathrm{inc} = T_\mathrm{inc}^{-1}T_\mathrm{refl}T_\mathrm{inc}\vec{\dot E}_\mathrm{inc} = | |||
\begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix} | |||
\begin{bmatrix} | |||
1 & 0 & 0 \\ | |||
0 & \cos(\pi - 2 \varphi_1) & \sin(\pi - 2 \varphi_1) \\ | |||
0 & -\sin(\pi - 2 \varphi_1) & \cos(\pi - 2 \varphi_1) | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
\rho_\mathrm{s} & 0 & 0 \\ | |||
0 & \rho_\mathrm{p} & 0 \\ | |||
0 & 0 & 1 | |||
\end{bmatrix} | |||
\begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix}^T</math>. | |||
''То есть, если падение волны не нормально плоскости отражающей поверхности, то,'' после упрощения, | |||
<math>\ | :<math>Y_\mathrm{refl} = | ||
\begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix} | |||
\begin{bmatrix} | |||
\rho_\mathrm{s} & 0 & 0 \\ | |||
0 & -\rho_\mathrm{p}\cos 2 \varphi_1 & \sin 2 \varphi_1 \\ | |||
0 & -\rho_\mathrm{p}\sin 2 \varphi_1 & -\cos 2 \varphi_1 | |||
\end{bmatrix} | |||
\begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix}^T</math>. | |||
<math>\ | ''Таким образом, напряженность электрического поля волнового элемента в результате его <math>m</math> отражений и <math>m + 1</math> прохождений в (различных изотропных) средах рассчитывается по формуле'' | ||
:<math>\vec{E} = y_{m+1} \left(\prod_{j=1}^m Y_j y_j\right) \vec{E}_0 r_0 = \prod_{j=1}^{m} Y_j \cdot \prod_{j=1}^{m + 1} y_j \cdot \vec{E}_0 r_0 = \prod_{j=1}^{m} Y_j \cdot \frac{e^{-i\sum_{j=1}^{m+1} k_j r_j}}{\sum_{j=1}^{m+1} r_j}</math>. | |||
=Метод реализации= | |||
Напряженность поля - реализуется трехкомпонентным комплексным вектором <math>\vec{\dot E}=\begin{pmatrix}\dot E_x & \dot E_y & \dot E_z\end{pmatrix}^T</math>. | |||
<math>\ | Состояние объекта, реализующего волновой элемент, задается: | ||
* <math>\vec{\varphi}_0 = \vec{\dot E}_0 r_0</math>, где <math>r_0</math> - расстояние в дальней зоне источника, на котором снято значение напряженности <math>\vec{\dot E}_0</math>[[Распространение_радиоволн_ВЧ/Первичный источник|первичного источника]]; | |||
* <math>\omega</math> - круговая частота волнового элемента; | |||
* <math>r_{\sum} = \sum_{j=0}^m r_j</math> - расстояние, пройденное в общем волновым элементом от первичного источника до его текущего расположения; | |||
* <math>\varphi_{\sum} = \sum_{j=0}^m k_j r_j</math> - фазовый сдвиг, которому подвергся волновой элемент в результате прохождения им расстояния <math>r_{\sum}</math>; | |||
* <math>Y_{\prod}=\prod_{j=1}^n Y_j</math> - матрица, реализующая отражение вектора напряженности. | |||
<math> | Тогда напряженность волнового элемента после всех распространений и отражений будет | ||
:<math>E=Y_{\prod}\frac{e^{-i\varphi_{\sum}}}{r_{\sum}}</math>. | |||
==Методы== | |||
< | * <tt>Изменить по пробегу(Пробег, Комплексное волновое число)</tt> | ||
* <tt>Изменить по отражению(КДП_1*, КМП_1**, КДП_2, КМП_2, Вектор(Направление луча), Вектор(Нормаль грани))</tt>=== | |||
<tt>*</tt> - комплексная диэлектрическая проницаемость, | |||
<tt>**</tt> - комплексная магнитная проницаемость. | |||
Текущая версия на 03:28, 13 октября 2018
Трехкомпонентный комплексный вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E} =\begin{pmatrix} \dot E_{x} \\ \dot E_{y} \\ \dot E_{z}\end{pmatrix},} который задается волновым элементом, порождаемым источником Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S , в результате распространения и отражений в среде.
Вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}} рассчитывается путем вычисления результирующих потерь при отражениях и распространении от источника следующим образом.
Модель распространения
Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_0} - дальняя зона, расстояние, на котором для источника Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S снята начальная напряженность Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E_0}} .
В результате распространения излученного элемента волны на расстояние Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_1} напряженность поля падает в Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_1 e^{ikr_1}} раз, становясь равной
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}\left(r_1\right)=\vec{\dot E_0}r_0 y_1 \left(r_1\right) = \vec{\dot E_0}\frac{r_0}{r_1}e^{-ikr_1}} , где:
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y_1 \left(r_1\right) = \frac{1}{r_1}e^{-ikr_1}} - скалярный коэффициент падения амплитуды напряженности при распространении волнового элемента в связи со сферическим расхождением волны,
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot k = \omega \sqrt{\dot \varepsilon \dot \mu}}
- комплексное волновое число
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \varepsilon = \varepsilon' - i \varepsilon''}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \mu= \mu' - i \mu''}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot k= k' - i k''}
Таким образом Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}\left(r_1\right) = \vec{\dot E_0} \frac{r_0}{r_1}e^{-k''r_1}e^{-ik'r_1}} .
Здесь первая экспонента является коэффициентом поглощения среды на расстоянии Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_1} , а
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle L = k''20 \lg e} - погонным затуханием среды [дБ/м]
В частности, при отсутствии инерционности поляризации и намагничивания Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha = 0,~\beta=0} :
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle k'=k=\omega \sqrt{\varepsilon \mu},~k''=\frac {\sigma}{2} \sqrt \frac {\mu}{\varepsilon}} .
Тогда, в результате распространения волнового элемента на расстояние Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_1 + r_2} от источника в одной и той же изотропной среде, результирующая напряженность станет равной
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\vec {\dot {E}}}\left(r_{1},r_{2}\right)={\vec {{\dot {E}}_{0}}}r_{0}y\left(r_{1},r_{2}\right)={\vec {{\dot {E}}_{0}}}r_{0}y_{1}\left(r_{1},r_{2}\right)\left(r_{1},r_{2}\right)y_{2}\left(r_{1},r_{2}\right)} ,
где Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y_1\left(r_1, r_2\right) = \left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{1}{2}}\frac{e^{-ikr_1}}{r_1}} , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y'_2\left(r_1, r_2\right) = \left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{1}{2}}\frac{e^{-ikr_2}}{r_2}} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y\left(r_1, r_2\right) = y_1\left(r_1, r_2\right)y_2\left(r_1, r_2\right)=\left(\frac{r_1 r_2}{r_1 + r_2}\right)^{\frac{2}{2}}\frac{e^{-ikr_1}e^{-ikr_2}}{r_1 r_2} = \frac{e^{-ik\left(r_1 + r_2\right)}}{r_1 + r_2}} .
В более общем случае
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}\left(r_1, \dots, r_n\right) = \vec{\dot E_0}r_0 y\left(r_1, \dots, r_n\right)=\vec{\dot E_0}r_0\prod_{j=1}^{n}y_j\left(r_1, \dots, r_n\right)= \vec{\dot E_0}\frac{r_0}{\sum_{i=1}^{n} r_i}e^{-i\left(\sum_{i=1}^{n} k_i r_i\right)}} ,
где Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y_j\left(r_1, \dots, r_n\right) = \left(\frac{\prod_{j'=1}^{n}r_{j'}}{\sum_{j'=1}^{n}r_{j'}}\right)^\frac{1}{n}\frac{e^{-ik_jr_j}}{r_j}} .
Модель отражения
Пусть электрическая напряженность волнового элемента, падающего на плоскую поверхность с нормалью Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{n}} , задается некоторым комплексным вектором Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}_\mathrm{inc}} . Пусть эта поверхность является границей раздела двух сред.
- среды с четверкой параметров Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left \{ \dot \varepsilon_1,~\dot \mu_1,~\dot k_1,~\dot Z_1 \right \}} , в которой распространяется падающая волна, и
- среды с четверкой параметров Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left \{ \dot \varepsilon_2,~\dot \mu_1,~\dot k_2,~\dot Z_2 \right \}} , на границу которой падает волна.
Соответственно, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varphi_1} - угол падения (и отражения), а угол Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varphi_2} - угол преломления.
Здесь:
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \varepsilon = \varepsilon \cos \alpha - i ( \frac{\sigma}{\omega} + \varepsilon \sin \alpha)}
- комплексная диэлектрическая проницаемость, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon} - диэлектрическая проницаемость среды,
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \sigma - проводимость среды,
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega - круговая частота волны,
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \alpha - угол диэлектрических потерь;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \mu = \mu \cos \beta - i \mu \sin \beta}
- комплексная магнитная проницаемость, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mu} - магнитная проницаемость среды,
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \beta - угол магнитных потерь;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot k = \omega \sqrt{\dot \varepsilon \dot \mu}} - комплексное волновое число;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot Z = \sqrt{\frac{\dot \mu}{\dot \varepsilon}}} - комплексное волновое сопротивление;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n_1\sin\varphi_1=n_2\sin\varphi_2}
согласно закону Снеллиуса, причем
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n=\frac{k}{\omega}=\sqrt{\mu\varepsilon}} - коэффициент преломления соответствующей среды.
Тогда коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля) соответственно:
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho_\mathrm{s} = \frac{Z_2 \cos \varphi_1 - Z_1 \cos \varphi_2}{Z_2 \cos \varphi_2 + Z_1 \cos \varphi_1}, }
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho_\mathrm{p} = \frac{Z_2 \cos \varphi_2 - Z_1 \cos \varphi_1}{Z_2 \cos \varphi_1 + Z_1 \cos \varphi_2}, }
Если направляющий вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}} луча параллелен нормали к отражающей поверхности, для расчета отраженной волны необходимо и достаточно аддитивно обратить вектор электрической напряженности Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}_\mathrm{inc}} падающей на поверхность волны и умножить этот вектор на скаляр, получаемый из приведенных выше формул Френеля для случая Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varphi_1 = \varphi_2 = 0} , т.е.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}_\mathrm{refl} = Y_\mathrm{refl}\vec{\dot E}_\mathrm{inc} = \begin{bmatrix} -\rho & 0 & 0 \\ 0 & -\rho & 0 \\ 0 & 0 & -\rho \end{bmatrix}} ,
где Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho=\frac{Z_2-Z_1}{Z_2+Z_1}} .
То есть для случая нормального падения на отражающую поверхность
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Y_\mathrm{refl} = \begin{bmatrix} -\rho & 0 & 0 \\ 0 & -\rho & 0 \\ 0 & 0 & -\rho \end{bmatrix}} .
Рассмотрим случай, когда направляющий вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}} луча не параллелен нормали к отражающей поверхности.
Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E'}_\mathrm{inc} = T_\mathrm{inc}\vec{\dot E}_\mathrm{inc}} - вектор электрической напряженности падающей на поверхность волны. Вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E'}_\mathrm{inc}} выражен в базисе Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \langle\vec{e_0},\vec{e_1},\vec{e_2}\rangle} , заданном так, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{e_0}} определяет направление, перпендикулярное плоскости падения волны, т.е. плоскости, которой принадлежат нормаль Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{n}} к отражающей поверхности и направляющий вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}} луча; вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{e_1}} задает направление, перпендикулярное Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{e_0}} и одновременно перпендикулярное Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}} ; а вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{e_2}} сонаправлен Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}} . Тогда выраженный в таком базисе вектор электрической напряженности, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E'}_\mathrm{inc}} , будет иметь три компоненты, первая из которых задает перпендикулярно поляризованную часть напряженности Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}_\mathrm{inc}} , вторая - параллельно поляризованную часть, а третья компонента вектора Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E'}_\mathrm{inc}} будет равна нулю как компонента, параллельная вектору Пойнтинга. Поэтому для расчета электрической напряженности отраженной волны достаточно умножить первую компоненту Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E'}_\mathrm{inc}} на Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho_\mathrm{s}} , вторую компоненту - на Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho_\mathrm{p}} , а третью - проигнорировать (или умножить имеющийся в ней ноль на произвольное значение).
Тогда Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}_\mathrm{inc} = \begin{bmatrix}\vec{e_0} & \vec{e_1} & \vec{e_2}\end{bmatrix}\vec{\dot E'}_\mathrm{inc}} , поэтому Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T_\mathrm{inc}=\begin{bmatrix}\vec{e_0} & \vec{e_1} & \vec{e_2}\end{bmatrix}^{-1}} .
При этом вектора базиса можно расчитать, как указано выше, с помощью векторного произведения:
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{e_0}=\vec{v}\times\vec{n}} ;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{e_1}=\vec{v}\times\left(\vec{v}\times\vec{n}\right)} ;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{e_2}=\vec{v}} .
Как указано выше, базис Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \langle\vec{e_0},\vec{e_1},\vec{e_2}\rangle} ортогонален, поэтому матрица Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T_\mathrm{inc}} также является ортогональной, и поэтому Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T_\mathrm{inc}^{-1}=T_\mathrm{inc}^T} .
Тогда вектор напряженности отраженной волны, в мировых координатах, равен
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}_\mathrm{refl} = Y_\mathrm{refl}\vec{E}_\mathrm{inc} = T_\mathrm{inc}^{-1}T_\mathrm{refl}T_\mathrm{inc}\vec{\dot E}_\mathrm{inc} = \begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\pi - 2 \varphi_1) & \sin(\pi - 2 \varphi_1) \\ 0 & -\sin(\pi - 2 \varphi_1) & \cos(\pi - 2 \varphi_1) \end{bmatrix} \begin{bmatrix} \rho_\mathrm{s} & 0 & 0 \\ 0 & \rho_\mathrm{p} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix}^T} .
То есть, если падение волны не нормально плоскости отражающей поверхности, то, после упрощения,
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Y_\mathrm{refl} = \begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix} \begin{bmatrix} \rho_\mathrm{s} & 0 & 0 \\ 0 & -\rho_\mathrm{p}\cos 2 \varphi_1 & \sin 2 \varphi_1 \\ 0 & -\rho_\mathrm{p}\sin 2 \varphi_1 & -\cos 2 \varphi_1 \end{bmatrix} \begin{bmatrix} \vec{e_0} & \vec{e_1} & \vec{e_2} \end{bmatrix}^T} .
Таким образом, напряженность электрического поля волнового элемента в результате его Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} отражений и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m + 1} прохождений в (различных изотропных) средах рассчитывается по формуле
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{E} = y_{m+1} \left(\prod_{j=1}^m Y_j y_j\right) \vec{E}_0 r_0 = \prod_{j=1}^{m} Y_j \cdot \prod_{j=1}^{m + 1} y_j \cdot \vec{E}_0 r_0 = \prod_{j=1}^{m} Y_j \cdot \frac{e^{-i\sum_{j=1}^{m+1} k_j r_j}}{\sum_{j=1}^{m+1} r_j}} .
Метод реализации
Напряженность поля - реализуется трехкомпонентным комплексным вектором Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}=\begin{pmatrix}\dot E_x & \dot E_y & \dot E_z\end{pmatrix}^T} .
Состояние объекта, реализующего волновой элемент, задается:
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\varphi}_0 = \vec{\dot E}_0 r_0} , где Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_0} - расстояние в дальней зоне источника, на котором снято значение напряженности Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E}_0} первичного источника;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega - круговая частота волнового элемента;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_{\sum} = \sum_{j=0}^m r_j} - расстояние, пройденное в общем волновым элементом от первичного источника до его текущего расположения;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varphi_{\sum} = \sum_{j=0}^m k_j r_j} - фазовый сдвиг, которому подвергся волновой элемент в результате прохождения им расстояния Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_{\sum}} ;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Y_{\prod}=\prod_{j=1}^n Y_j} - матрица, реализующая отражение вектора напряженности.
Тогда напряженность волнового элемента после всех распространений и отражений будет
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E=Y_{\prod}\frac{e^{-i\varphi_{\sum}}}{r_{\sum}}} .
Методы
- Изменить по пробегу(Пробег, Комплексное волновое число)
- Изменить по отражению(КДП_1*, КМП_1**, КДП_2, КМП_2, Вектор(Направление луча), Вектор(Нормаль грани))===
* - комплексная диэлектрическая проницаемость, ** - комплексная магнитная проницаемость.