Распространение радиоволн ВЧ/Рей-трейсинг: различия между версиями
Nigiluk (обсуждение | вклад) |
|||
| (не показано 20 промежуточных версий 2 участников) | |||
| Строка 60: | Строка 60: | ||
::<math>\frac{dn}{dh}=grad~n</math> - изменение коэффициента преломления с высотой. | ::<math>\frac{dn}{dh}=grad~n</math> - изменение коэффициента преломления с высотой. | ||
:<math>r=\sqrt{x^{2}+y^{2}}</math> - расстояние до точки с высотой <math>h(x,y)</math>. | :<math>r=\sqrt{x^{2}+y^{2}}</math> - расстояние до точки с высотой <math>h(x,y)</math>. | ||
==Основной цикл программы | Вариант 1== | ==Основной цикл программы | Вариант 1== | ||
| Строка 109: | Строка 108: | ||
==Основной цикл программы | Вариант 2== | ==Основной цикл программы | Вариант 2== | ||
'''Геометрическая модель (рей-трейсинг 2)'''. | |||
''Наследует свойства [[Распространение радиоволн ВЧ/Геометрическая модель|Геометрической модели]].'' | |||
* Предикат завершения(). При <math>i = 0</math> возвращает истину, иначе возвращает значение функции SubApprox для результатов моделирования не предыдущем и на текущем этапах, а также для включаемого отклонения <math>\Delta</math> и допустимого процента точек <math>k</math>. | |||
===Предусловия=== | ===Предусловия=== | ||
* <math>G</math> - входное описание среды распространения моделируемого поля, заданное [[Распространение радиоволн ВЧ/Геометрическая модель|геометрической моделью]]. | * <math>G</math> - входное описание среды распространения моделируемого поля, заданное [[Распространение радиоволн ВЧ/Геометрическая модель|геометрической моделью]]. | ||
* <math>\Omega</math> - список частот, на которых необходимо провести моделирование. | |||
* <math>E_{end}</math> - критическое значение напряженности, на котором дальнейшая трассировка луча прекращается. | * <math>E_{end}</math> - критическое значение напряженности, на котором дальнейшая трассировка луча прекращается. | ||
* <math>\Delta</math> - | * <math>\Delta</math> - критерий разности между текущим и предыдущим результатом моделирования, при которой можно считать, что поле промоделированно точно. | ||
===Основное течение=== | ===Основное течение=== | ||
#<math>\forall ~ \omega_n \in \Omega</math> | |||
##<math>i \leftarrow 0</math> | |||
##Pre_SCP <math> \leftarrow</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Множество контрольных точек|Множество контрольных точек(<math>\omega_n</math>)]]</tt> ''//Копирование состояния до изменения''. | |||
##Set_event <math>\leftarrow</math><tt> Preprocessing(<math>G,~i,~\omega_n</math>)</tt> | |||
##<math>\forall ~ (s_j,~\theta,~\varphi) \in </math> Set_event | |||
###Ray <math>\leftarrow</math><tt> [[Распространение радиоволн ВЧ/Луч|Луч()]].Создать([[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]], <math>\theta,~\varphi,~\omega_n</math>)</tt> | |||
###<tt>Trace(Ray, [[Распространение радиоволн ВЧ/Геометрическая модель|G]], <math>E_{end}</math>)</tt> | |||
##<tt>Postprocessing([[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Множество контрольных точек|Множество контрольных точек(<math>\omega_n</math>)]])</tt> | |||
##SAcheck <math>\leftarrow</math><tt> SucApprox([[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Множество контрольных точек|Множество контрольных точек(<math>\omega_n</math>)]], Pre_SCP, <math>\Delta</math>)</tt> | |||
##Если SAcheck | |||
###<math>i \leftarrow i+1</math> | |||
###Переход на 1.2 | |||
#ВЫХОД | |||
===<tt>[Таблица событий] <math>\leftarrow</math> Preprocessing(Геометрическая модель, Номер итерации, Частота)</tt>=== | |||
Функция создает таблицу событий, необходимых обработать. В качестве событий - испускаемые моделью лучи на данной частоте. | |||
#<math>T \leftarrow</math> Пустой односвязный список значений <math>(s_j,~\theta,~\varphi)</math>. | |||
#<math>G \leftarrow</math> Геометрическая модель. | |||
#<math>i \leftarrow</math> Номер итерации | |||
#<math>\omega \leftarrow</math> Частота | |||
#<math>\forall ~ s_j \in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Первичный источник|Множество первичных источников()]]</tt> | |||
##Если <tt> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].[[Распространение радиоволн ВЧ/Тип антенны|Тип антенны()]].[[Распространение радиоволн ВЧ/Амплитудно-частотная характеристика|Амплитудно-частотная характеристика(<math>\omega</math>)]]</tt> <math>\ne 0</math> | |||
###<math>\theta \leftarrow 0</math> | |||
###<math>\zeta_{\theta} \leftarrow 0</math> | |||
###Пока <math>\theta < \pi</math> | |||
####<math>\varphi \leftarrow 0</math> | |||
####<math>\zeta_{\varphi} \leftarrow 0</math> | |||
####Пока <math>\varphi<2\pi</math> | |||
#####Если <math>i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0</math> | |||
######<math>T</math>.Добавить<math>(s_j,~\theta,~\varphi)</math> | |||
#####<math>\varphi \leftarrow \varphi + \frac{\Delta_{\varphi} (s_j,~\theta,~\varphi)}{2^i}</math> | |||
#####<math>\zeta_{\varphi} \leftarrow \zeta_{\varphi}+1</math> | |||
####<math>\theta \leftarrow \theta + \frac{\Delta_{\theta} (s_j,~\theta)}{2^i}</math> | |||
####<math>\zeta_{\theta} \leftarrow \zeta_{\theta}+1</math> | |||
#Вернуть Массив(<math>T</math>) | |||
Если <math>\Delta_{\varphi} (s_j,~\theta,~\varphi) = {\rm const}</math>, и <math>\Delta_{\theta} (s_j,~\theta) = {\rm const}</math>, то есть углы распределены равномерно, таблица может быть реализована в виде массива значений <math>(s_j,~\theta,~\varphi)</math>, элементы которого могут заполняться параллельно, без синхронизации. Если же размер таблицы заранее не определен (общий случай), то таблица реализуется связанным списком, добавление элементов в который должно защищаться мьютексом на шаге 4.1.3.1.3.1.1, а алгоритм на заключительном шаге преобразует связанный список в массив с произвольным доступом. Второй путь при параллельном выполнении - создавать таблицы в локальной памяти потока, после выполнения которых - объединять таблицы в массив в основном потоке. | |||
====Параллельная форма==== | |||
Параллельное выполнение в общем случае возможно только цикла, перебирающего первичные источники (шаг 4), так как распределение углов заранее не определено. | |||
Пусть <math>P>0</math> - число потоков, выполняющих функцию. Пусть <math>T'</math> - массив изначально пустых связанных списков троек <math>(s_j,~\theta,~\varphi)</math>, так, что <math>T'_i</math> - <math>i</math>-тый список массива, <math>0\le i<P</math>. | |||
#<math>i \leftarrow</math> Номер итерации | |||
#<math>\omega \leftarrow</math> Частота | |||
#<math>T'\leftarrow</math>Создать массив. | |||
#<math>\forall ~ s_j \in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Первичный источник|Множество первичных источников()]]</tt> | #<math>\forall ~ s_j \in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Первичный источник|Множество первичных источников()]]</tt> | ||
##<math>\ | ##<math>t\leftarrow</math> индекс потока. | ||
##Если <tt> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].[[Распространение радиоволн ВЧ/Тип антенны|Тип антенны()]].[[Распространение радиоволн ВЧ/Амплитудно-частотная характеристика|Амплитудно-частотная характеристика(<math>\omega</math>)]]</tt> <math>\ne 0</math> | |||
###<math>\theta \leftarrow 0</math> | ###<math>\theta \leftarrow 0</math> | ||
###<math>\zeta_{\theta} \leftarrow 0</math> | ###<math>\zeta_{\theta} \leftarrow 0</math> | ||
###Пока <math>\theta < \pi</math> | ###Пока <math>\theta < \pi</math> | ||
####<math>\varphi \leftarrow 0</math> | |||
####<math>\zeta_{\varphi} \leftarrow 0</math> | |||
####Пока <math>\varphi<2\pi</math> | |||
#####Если <math>i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0</math> | |||
######<math>T'_t</math>.Добавить<math>(s_j,~\theta,~\varphi)</math> | |||
###### | #####<math>\varphi \leftarrow \varphi + \frac{\Delta_{\varphi} (s_j,~\theta,~\varphi)}{2^i}</math> | ||
#####<math>\zeta_{\varphi} \leftarrow \zeta_{\varphi}+1</math> | |||
####<math>\theta \leftarrow \theta + \frac{\Delta_{\theta} (s_j,~\theta)}{2^i}</math> | |||
####<math>\theta \leftarrow \theta + \frac{\Delta_{\theta} (\theta)}{2^i}</math> | |||
####<math>\zeta_{\theta} \leftarrow \zeta_{\theta}+1</math> | ####<math>\zeta_{\theta} \leftarrow \zeta_{\theta}+1</math> | ||
# | #Вернуть Массив<math>\left(\bigsqcup_{t=0}^{P-1}T'_t\right)</math> | ||
===<tt>Trace</tt>=== | ===<tt>Trace</tt>=== | ||
Функция трассирует луч через геометрическую модель и и фиксирует его прохождение вблизи контрольной точки. | Функция трассирует луч через геометрическую модель и и фиксирует его прохождение вблизи контрольной точки. | ||
# | |||
#<math>R\leftarrow \infty</math> | |||
#<math>T\leftarrow </math> NaN | |||
#<math>\forall ~ f_m\in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].Множество отражающих объектов()</tt> | #<math>\forall ~ f_m\in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].Множество отражающих объектов()</tt> | ||
##<math>\forall ~ t_{mn} \in f_m</math><tt>.Множество отражающих поверхностей()</tt> | ##<math>\forall ~ t_{mn} \in f_m</math><tt>.Множество отражающих поверхностей()</tt> | ||
###<tt><math> | ###<tt><math>p \leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Пересечение([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость())</tt> | ||
###Если <tt>[[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Принадлежность(<math> | ###Если <tt>[[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Принадлежность(<math>p</math>)</tt> | ||
#### | ####<math>r\leftarrow</math><tt> [[Распространение радиоволн ВЧ/Луч|Ray]].Пробег(<math>p</math>)</tt> | ||
####Если | ####Если <math>r < R</math> | ||
##### | #####<math>R \leftarrow r</math> | ||
#####<math> | #####<math>T \leftarrow t_{mn}</math> | ||
#####<math>P \leftarrow | #####<math>P \leftarrow p</math> | ||
#<math>\forall ~ | #<math>\forall ~ O_k \in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Плоскость вывода результатов|Множество плоскостей вывода результатов()]]</tt> | ||
## | ##<tt><math>p \leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Пересечение([[Распространение радиоволн ВЧ/Плоскость вывода результатов|<math>O_k</math>]].Плоскость())</tt> | ||
### | ##Если <tt>[[Распространение радиоволн ВЧ/Плоскость вывода результатов|<math>O_k</math>]].Принадлежность(<math>p</math>)</tt> | ||
# | ###<math>r\leftarrow</math><tt> [[Распространение радиоволн ВЧ/Луч|Ray]].Пробег(<math>p</math>)</tt> | ||
## | ###Если <math>r < R</math> | ||
## | ####<math>\rho \leftarrow</math><tt> [[Распространение радиоволн ВЧ/Плоскость вывода результатов|<math>O_k</math>]].Ближайшая контрольная точка(<math>p</math>)</tt> | ||
##< | ####<tt><math>\rho</math>.Зарегистрировать([[Распространение радиоволн ВЧ/Луч|Ray]], <math>r</math>, [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]])</tt> | ||
#Если <math>T \not\equiv</math> NaN | |||
#<tt>Trace(Ray, [[Распространение радиоволн ВЧ/Геометрическая модель|G]], <math>E_{end}</math>)</tt> | ##<tt><math>\gamma \leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Угол пересечения([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>T</math>]].Плоскость())</tt> | ||
##<tt>[[Распространение радиоволн ВЧ/Луч|Ray]].Отразить(<math>T,~P,~R,~\gamma</math>, [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]])</tt> | |||
##Если <tt>[[Распространение радиоволн ВЧ/Луч|Ray]].Напряженность <math> >E_{end} </math></tt> | |||
###<tt>Trace(Ray, [[Распространение радиоволн ВЧ/Геометрическая модель|G]], <math>E_{end}</math>)</tt> | |||
===<tt>Postprocessing</tt>=== | ===<tt>Postprocessing</tt>=== | ||
| Строка 170: | Строка 218: | ||
====Сложность==== | ====Сложность==== | ||
====Возможности распараллеливания==== | ====Возможности распараллеливания==== | ||
<graphviz size=500px> | |||
digraph ray_tracing_EM_parallel_run{ | |||
rankdir=LR; | |||
node[fontsize=14]; | |||
edge[fontsize=14]; | |||
G0[label="ВХОД"]; | |||
G1[label="1"]; | |||
G2_1[label="2"]; | |||
G3_1[label="3"]; | |||
G4_1[label="4"]; | |||
G5_1[label="5"]; | |||
G2_2[label="2"]; | |||
G3_2[label="3"]; | |||
G4_2[label="4"]; | |||
G5_2[label="5"]; | |||
G6_1_1[label="6"]; | |||
G6_1_2[label="6"]; | |||
G6_2_1[label="6"]; | |||
G6_2_2[label="6"]; | |||
G7_1_1_1[label="7.1"]; | |||
G7_3_1_1[label="7.3"]; | |||
G7_4_1_1_1[label="7.4"]; | |||
G7_4_1_1_2[label="7.4"]; | |||
G7_5_1_1_1_1[label="7.5"]; | |||
G7_13_1_1_1_1[label="7.13"]; | |||
G7_5_1_1_1_2[label="7.5"]; | |||
G7_13_1_1_1_2[label="7.13"]; | |||
G7_5_1_1_2_1[label="7.5"]; | |||
G7_13_1_1_2_1[label="7.13"]; | |||
G7_5_1_1_2_2[label="7.5"]; | |||
G7_13_1_1_2_2[label="7.13"]; | |||
G7_14_1_1_1[label="7.14"]; | |||
G7_14_1_1_2[label="7.14"]; | |||
G7_15_1_1[label="7.15"]; | |||
G7_16_1_1[label="7.16"]; | |||
G7_17_1_1_1[label="7.17"]; | |||
G7_24_1_1_1[label="7.24"]; | |||
G7_17_1_1_2[label="7.17"]; | |||
G7_24_1_1_2[label="7.24"]; | |||
G7_25_1_1[label="7.25"]; | |||
G7_32_1_1[label="7.32"]; | |||
G7_1_1_2[label="7.1"]; | |||
G7_3_1_2[label="7.3"]; | |||
G7_4_1_2_1[label="7.4"]; | |||
G7_4_1_2_2[label="7.4"]; | |||
G7_5_1_2_1_1[label="7.5"]; | |||
G7_13_1_2_1_1[label="7.13"]; | |||
G7_5_1_2_1_2[label="7.5"]; | |||
G7_13_1_2_1_2[label="7.13"]; | |||
G7_5_1_2_2_1[label="7.5"]; | |||
G7_13_1_2_2_1[label="7.13"]; | |||
G7_5_1_2_2_2[label="7.5"]; | |||
G7_13_1_2_2_2[label="7.13"]; | |||
G7_14_1_2_1[label="7.14"]; | |||
G7_14_1_2_2[label="7.14"]; | |||
G7_15_1_2[label="7.15"]; | |||
G7_16_1_2[label="7.16"]; | |||
G7_17_1_2_1[label="7.17"]; | |||
G7_24_1_2_1[label="7.24"]; | |||
G7_17_1_2_2[label="7.17"]; | |||
G7_24_1_2_2[label="7.24"]; | |||
G7_25_1_2[label="7.25"]; | |||
G7_32_1_2[label="7.32"]; | |||
G7_1_2_1[label="7.1"]; | |||
G7_3_2_1[label="7.3"]; | |||
G7_4_2_1_1[label="7.4"]; | |||
G7_4_2_1_2[label="7.4"]; | |||
G7_5_2_1_1_1[label="7.5"]; | |||
G7_13_2_1_1_1[label="7.13"]; | |||
G7_5_2_1_1_2[label="7.5"]; | |||
G7_13_2_1_1_2[label="7.13"]; | |||
G7_5_2_1_2_1[label="7.5"]; | |||
G7_13_2_1_2_1[label="7.13"]; | |||
G7_5_2_1_2_2[label="7.5"]; | |||
G7_13_2_1_2_2[label="7.13"]; | |||
G7_14_2_1_1[label="7.14"]; | |||
G7_14_2_1_2[label="7.14"]; | |||
G7_15_2_1[label="7.15"]; | |||
G7_16_2_1[label="7.16"]; | |||
G7_17_2_1_1[label="7.17"]; | |||
G7_24_2_1_1[label="7.24"]; | |||
G7_17_2_1_2[label="7.17"]; | |||
G7_24_2_1_2[label="7.24"]; | |||
G7_25_2_1[label="7.25"]; | |||
G7_32_2_1[label="7.32"]; | |||
G7_1_2_2[label="7.1"]; | |||
G7_3_2_2[label="7.3"]; | |||
G7_4_2_2_1[label="7.4"]; | |||
G7_4_2_2_2[label="7.4"]; | |||
G7_5_2_2_1_1[label="7.5"]; | |||
G7_13_2_2_1_1[label="7.13"]; | |||
G7_5_2_2_1_2[label="7.5"]; | |||
G7_13_2_2_1_2[label="7.13"]; | |||
G7_5_2_2_2_1[label="7.5"]; | |||
G7_13_2_2_2_1[label="7.13"]; | |||
G7_5_2_2_2_2[label="7.5"]; | |||
G7_13_2_2_2_2[label="7.13"]; | |||
G7_14_2_2_1[label="7.14"]; | |||
G7_14_2_2_2[label="7.14"]; | |||
G7_15_2_2[label="7.15"]; | |||
G7_16_2_2[label="7.16"]; | |||
G7_17_2_2_1[label="7.17"]; | |||
G7_24_2_2_1[label="7.24"]; | |||
G7_17_2_2_2[label="7.17"]; | |||
G7_24_2_2_2[label="7.24"]; | |||
G7_25_2_2[label="7.25"]; | |||
G7_32_2_2[label="7.32"]; | |||
G8_1[label="8"]; | |||
G14_1[label="14"]; | |||
G8_2[label="8"]; | |||
G14_2[label="14"]; | |||
G15[label="15"]; | |||
SKIP_1[label="...", shape="none"]; | |||
SKIP_2[label="...", shape="none"]; | |||
SKIP_3[label="...", shape="none"]; | |||
SKIP_4[label="...", shape="none"]; | |||
SKIP_5[label="...", shape="none"]; | |||
SKIP_6[label="...", shape="none"]; | |||
SKIP_7[label="...", shape="none"]; | |||
SKIP_8[label="...", shape="none"]; | |||
SKIP_9[label="...", shape="none"]; | |||
SKIP_10[label="...", shape="none"]; | |||
//SKIP_11[label="...", shape="none"]; | |||
SKIP_12[label="...", shape="none"]; | |||
SKIP_13[label="...", shape="none"]; | |||
SKIP_14[label="...", shape="none"]; | |||
SKIP_15[label="...", shape="none"]; | |||
SKIP_16[label="...", shape="none"]; | |||
SKIP_17[label="...", shape="none"]; | |||
SKIP_18[label="...", shape="none"]; | |||
SKIP_19[label="...", shape="none"]; | |||
SKIP_20[label="...", shape="none"]; | |||
SKIP_21[label="...", shape="none"]; | |||
SKIP_22[label="...", shape="none"]; | |||
SKIP_23[label="...", shape="none"]; | |||
SKIP_24[label="...", shape="none"]; | |||
SKIP_25[label="...", shape="none"]; | |||
SKIP_26[label="...", shape="none"]; | |||
SKIP_27[label="...", shape="none"]; | |||
SKIP_28[label="...", shape="none"]; | |||
SKIP_29[label="...", shape="none"]; | |||
SKIP_30[label="...", shape="none"]; | |||
SKIP_31[label="...", shape="none"]; | |||
G0->G1->{G2_1, G2_2} | |||
G2_1->G3_1->G4_1->G5_1->{G6_1_1, G6_1_2} | |||
G6_1_1->G7_1_1_1 | |||
G6_1_2->G7_1_1_2 | |||
{G7_32_1_1, G7_32_1_2}->G8_1->SKIP_30->G14_1 | |||
G2_2->G3_2->G4_2->G5_2->{G6_2_1, G6_2_2} | |||
G6_2_1->G7_1_2_1 | |||
G6_2_2->G7_1_2_2 | |||
{G7_32_2_1, G7_32_2_2}->G8_2->SKIP_31->G14_2 | |||
{G14_1, G14_2}->G15->"ВЫХОД" | |||
G7_1_1_1->G7_3_1_1->{G7_4_1_1_1, G7_4_1_1_2} | |||
G7_4_1_1_1->{G7_5_1_1_1_1, G7_5_1_1_1_2} | |||
G7_5_1_1_1_1->SKIP_1->G7_13_1_1_1_1 | |||
G7_5_1_1_1_2->SKIP_2->G7_13_1_1_1_2 | |||
{G7_13_1_1_1_1, G7_13_1_1_1_2}->G7_14_1_1_1 | |||
G7_4_1_1_2->{G7_5_1_1_2_1, G7_5_1_1_2_2} | |||
G7_5_1_1_2_1->SKIP_3->G7_13_1_1_2_1 | |||
G7_5_1_1_2_2->SKIP_4->G7_13_1_1_2_2 | |||
{G7_13_1_1_2_1, G7_13_1_1_2_2}->G7_14_1_1_2 | |||
{G7_14_1_1_1, G7_14_1_1_2}->G7_15_1_1->G7_16_1_1->{G7_17_1_1_1, G7_17_1_1_2} | |||
G7_17_1_1_1->SKIP_5->G7_24_1_1_1 | |||
G7_17_1_1_2->SKIP_6->G7_24_1_1_2 | |||
{G7_24_1_1_1, G7_24_1_1_2}->G7_25_1_1->SKIP_15->G7_32_1_1 | |||
G7_1_1_2->G7_3_1_2->{G7_4_1_2_1, G7_4_1_2_2} | |||
G7_4_1_2_1->{G7_5_1_2_1_1, G7_5_1_2_1_2} | |||
G7_5_1_2_1_1->SKIP_18->G7_13_1_2_1_1 | |||
G7_5_1_2_1_2->SKIP_19->G7_13_1_2_1_2 | |||
{G7_13_1_2_1_1, G7_13_1_2_1_2}->G7_14_1_2_1 | |||
G7_4_1_2_2->{G7_5_1_2_2_1, G7_5_1_2_2_2} | |||
G7_5_1_2_2_1->SKIP_16->G7_13_1_2_2_1 | |||
G7_5_1_2_2_2->SKIP_17->G7_13_1_2_2_2 | |||
{G7_13_1_2_2_1, G7_13_1_2_2_2}->G7_14_1_2_2 | |||
{G7_14_1_2_1, G7_14_1_2_2}->G7_15_1_2->G7_16_1_2->{G7_17_1_2_1, G7_17_1_2_2} | |||
G7_17_1_2_1->SKIP_7->G7_24_1_2_1 | |||
G7_17_1_2_2->SKIP_8->G7_24_1_2_2 | |||
{G7_24_1_2_1, G7_24_1_2_2}->G7_25_1_2->SKIP_12->G7_32_1_2 | |||
G7_1_2_1->G7_3_2_1->{G7_4_2_1_1, G7_4_2_1_2} | |||
G7_4_2_1_1->{G7_5_2_1_1_1, G7_5_2_1_1_2} | |||
G7_5_2_1_1_1->SKIP_20->G7_13_2_1_1_1 | |||
G7_5_2_1_1_2->SKIP_21->G7_13_2_1_1_2 | |||
{G7_13_2_1_1_1, G7_13_2_1_1_2}->G7_14_2_1_1 | |||
G7_4_2_1_2->{G7_5_2_1_2_1, G7_5_2_1_2_2} | |||
G7_5_2_1_2_1->SKIP_22->G7_13_2_1_2_1 | |||
G7_5_2_1_2_2->SKIP_23->G7_13_2_1_2_2 | |||
{G7_13_2_1_2_1, G7_13_2_1_2_2}->G7_14_2_1_2 | |||
{G7_14_2_1_1, G7_14_2_1_2}->G7_15_2_1->G7_16_2_1->{G7_17_2_1_1, G7_17_2_1_2} | |||
G7_17_2_1_1->SKIP_9->G7_24_2_1_1 | |||
G7_17_2_1_2->SKIP_10->G7_24_2_1_2 | |||
{G7_24_2_1_1, G7_24_2_1_2}->G7_25_2_1->SKIP_13->G7_32_2_1 | |||
G7_1_2_2->G7_3_2_2->{G7_4_2_2_1, G7_4_2_2_2} | |||
G7_4_2_2_1->{G7_5_2_2_1_1, G7_5_2_2_1_2} | |||
G7_5_2_2_1_1->SKIP_24->G7_13_2_2_1_1 | |||
G7_5_2_2_1_2->SKIP_25->G7_13_2_2_1_2 | |||
{G7_13_2_2_1_1, G7_13_2_2_1_2}->G7_14_2_2_1 | |||
G7_4_2_2_2->{G7_5_2_2_2_1, G7_5_2_2_2_2} | |||
G7_5_2_2_2_1->SKIP_26->G7_13_2_2_2_1 | |||
G7_5_2_2_2_2->SKIP_27->G7_13_2_2_2_2 | |||
{G7_13_2_2_2_1, G7_13_2_2_2_2}->G7_14_2_2_2 | |||
{G7_14_2_2_1, G7_14_2_2_2}->G7_15_2_2->G7_16_2_2->{G7_17_2_2_1, G7_17_2_2_2} | |||
G7_17_2_2_1->SKIP_28->G7_24_2_2_1 | |||
G7_17_2_2_2->SKIP_29->G7_24_2_2_2 | |||
{G7_24_2_2_1, G7_24_2_2_2}->G7_25_2_2->SKIP_14->G7_32_2_2 | |||
} | |||
</graphviz> | |||
Текущая версия на 07:50, 14 февраля 2018
Модель
Алгоритм
Идея последовательного приближения
Идея заключается в последовательном удвоении числа элементарных модельных экспериментов. Это продолжится до тех пор, пока результат текущего моделирования не приблизится к результату моделирования на предыдущей итерации:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \left | F_i-F_{i-1} \right |<\Delta , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta - параметр моделирования, задаваемый пользователем.
Однако сравнение соседних итераций не дает достаточного условия на достижение заданной точности (основная причина этого - излучение по направлениям). Поэтому правильнее будет сравнивать итерации через одну, две и т.д.:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \left | F_i-F_{i-k} \right |<\Delta , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): k также будет задаваться пользователем.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i здесь - это параметр цикла, стоящего над циклами основной программы, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i=\overline{0:N} .
При равномерном увеличении числа направлений излучения от первичного источника в два раза путем деления на 2 соответствующего шага по углу в процессе увеличения Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i , только каждое второе направление будет новым, т.е. не учитанным на предыдущих итерациях. Другая половина будет повторять эксперименты, уже выполненные ранее. Поэтому в цикл основной программы введено дополнительное условие для учета этих повторений.
Шаги Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta_{\theta}\left(\theta\right) по азимуту и по зениту источника являются функциями от направления либо постоянными.
Угловой шаг дискретизации как функция ХН
Большинство современных вещательных систем используют панельные антенны с ограниченными углами раствора диаграммы направленности (ДН) в горизонтальной плоскости (до 120°) и очень малыми углами в вертикальной плоскости (до 20°). Соответственно, в таких системах происходит серьезное перераспределение излучаемой энергии в пространстве. Типичные коэффициенты усиления: 16-18 dBi. Поэтому одним из решений задачи оптимизации является использование динамического углового шага дискретизации Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta_{\theta},~\Delta_{\varphi} как функции от характеристики направленности источника.
Изменение частоты дискретизации Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega(\theta,\varphi, f) происходит по следующему закону:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega(\theta,\varphi, f) = \omega_{min} + k F(\theta,\varphi, f) , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): k = \omega_{max} - \omega_{min} - коэффициент девиации, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_{max} = \frac{1}{\arcsin\left(\frac{\lambda}{R_{max}}\right)}\approx\frac{R_{max}}{\lambda} - максимальное и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_{min} = \alpha\omega_{max} (для любого Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): 0 \leq \alpha \leq 1 ) минимальное значение частоты дискретизации;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R_{max} - максимальное расстояние от источника до границ модели;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): F - функция ХН;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta,~ \varphi - угол места и азимутальный угол;
- - частота излучения;
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \lambda - длина излучаемой волны.
Тогда шаг дискретизации (угол) будет меняться по следующим образом:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta_{\theta},~\Delta_{\varphi} = \frac {1} {\omega(\theta,\varphi)}
Общее кол-во лучей определяется выражением:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): N_{total} = \frac {1} {2 \pi^2} \int \limits_0^{\pi} \int \limits_0^{2 \pi} \omega(\theta,\varphi)~d \theta d \varphi
С учетом, что максимум ДН находится в Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta=0,~\varphi=0 , получим выражения:
,
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): N_{\varphi~total}(\theta) = \frac {1} {2 \pi} \int \limits_0^{2 \pi} \omega(\theta,\varphi)~d \varphi .
Инициализация геометрической модели
Перерасчет высот с учетом кривизны земли и рефракции радиоволн в тропосфере.
Входной параметр Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): h пересчитывается в соответствии с формулой:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): h'(x,y) = h(x,y)-\frac{-2 R_{eq}+\sqrt{(2 R_{eq})^{2}+4 r^{2}}}{2} \approx h(x,y)-\frac{r^{2}}{2 R_{eq}} , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R_{eq}=\frac{R_0}{1+R_0 \frac{dn}{dh}}
- эквивалентный радиус Земли, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R_0=6371 - радиус Земли (км),
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \frac{dn}{dh}=grad~n - изменение коэффициента преломления с высотой.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r=\sqrt{x^{2}+y^{2}} - расстояние до точки с высотой Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): h(x,y) .
Основной цикл программы | Вариант 1
Предусловия
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): G - входное описание среды распространения моделируемого поля, заданное геометрической моделью.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i - номер итерации моделирования, .
Основное течение
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \leftarrow G.Множество первичных источников()
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \colon ~\varnothing то ВЫХОД
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ s_j \in S
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \leftarrow S~ \backslash \left \{ s_j \right \}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ \omega_n \in
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Антенна().Тип антенны().Амплитудно-частотная характеристика()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta \leftarrow 0
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta < \pi \wedge (i=0 \vee \zeta_{\theta} \bmod 2 \neq 0)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\varphi} \leftarrow 0
- Если
- Position Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Антенна().Позиция()
- Ray Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Луч().Создать(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Антенна().Мировая система координат(Вектор))
- Distance Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow \infty
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ f_m\in
G.Множество отражающих объектов()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P' \leftarrow Ray.Пересечение(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} .Плоскость грани())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn}
.Принадлежность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P'
)
- Distance' Расстояние(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P' )
- Если Distance' Distance
- Distance Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Distance'
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t' \leftarrow t_{mn}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow P'
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- G.Множество контрольных точек()
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k \in
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Область регистрации луча Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\theta,~\varphi,~\frac{\Delta_{\theta} (\theta)}{2^i},~\frac{\Delta_{\varphi} (\theta, \varphi)}{2^i},
DistanceНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): )
- .Зарегистрировать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Напряженность, Расстояние(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k .Позиция()), G.Среда распространения())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k \in
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Область регистрации луча Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\theta,~\varphi,~\frac{\Delta_{\theta} (\theta)}{2^i},~\frac{\Delta_{\varphi} (\theta, \varphi)}{2^i},
DistanceНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): )
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.НапряженностьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\omega_n,~\theta,~\varphi
, Distance, G.Среда распространения()Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): )>E_{end}
- Angle Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Ray.Угол пересечения(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t' .Плоскость грани())
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s' \leftarrow Вторичный источник при рейтрейсинге.Создать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Напряженность, Distance, G.Среда распространения()Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): ), Angle, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): P,~t' )
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \leftarrow S \cup \{s'\}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi \leftarrow \varphi + \frac{\Delta_{\varphi} (\theta, \varphi)}{2^i}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\varphi} \leftarrow \zeta_{\varphi}+1
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta \leftarrow \theta + \frac{\Delta_{\theta} (\theta)}{2^i}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \zeta_{\theta} \leftarrow \zeta_{\theta}+1
- Переход на шаг 2
Свойства алгоритма
Сложность
Возможности распараллеливания
Основной цикл программы | Вариант 2
Геометрическая модель (рей-трейсинг 2). Наследует свойства Геометрической модели.
- Предикат завершения(). При Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i = 0} возвращает истину, иначе возвращает значение функции SubApprox для результатов моделирования не предыдущем и на текущем этапах, а также для включаемого отклонения Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta и допустимого процента точек Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): k .
Предусловия
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): G - входное описание среды распространения моделируемого поля, заданное геометрической моделью.
- - список частот, на которых необходимо провести моделирование.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E_{end} - критическое значение напряженности, на котором дальнейшая трассировка луча прекращается.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta - критерий разности между текущим и предыдущим результатом моделирования, при которой можно считать, что поле промоделированно точно.
Основное течение
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ \omega_n \in \Omega
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i \leftarrow 0
- Pre_SCP Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \leftarrow } G.Множество контрольных точек(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_n ) //Копирование состояния до изменения.
- Set_event Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Preprocessing(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G,~i,~\omega_n} )
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \forall ~ (s_j,~\theta,~\varphi) \in }
Set_event
- Ray Луч().Создать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta,~\varphi,~\omega_n} )
- Trace(Ray, G, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E_{end} )
- Postprocessing(G.Множество контрольных точек(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_n ))
- SAcheck Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow SucApprox(G.Множество контрольных точек(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_n ), Pre_SCP, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Delta )
- Если SAcheck
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): i \leftarrow i+1
- Переход на 1.2
- ВЫХОД
[Таблица событий] Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Preprocessing(Геометрическая модель, Номер итерации, Частота)
Функция создает таблицу событий, необходимых обработать. В качестве событий - испускаемые моделью лучи на данной частоте.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T \leftarrow} Пустой односвязный список значений Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)} .
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G \leftarrow} Геометрическая модель.
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle i\leftarrow } Номер итерации
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega \leftarrow Частота
- G.Множество первичных источников()
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Антенна().Тип антенны().Амплитудно-частотная характеристика(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega
) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ne 0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta \leftarrow 0
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\theta} \leftarrow 0
- Пока Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta < \pi
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi \leftarrow 0
- Пока Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi<2\pi
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T .ДобавитьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varphi \leftarrow \varphi + \frac{\Delta_{\varphi} (s_j,~\theta,~\varphi)}{2^i}}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\varphi} \leftarrow \zeta_{\varphi}+1
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta \leftarrow \theta + \frac{\Delta_{\theta} (s_j,~\theta)}{2^i}}
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): \zeta_{\theta} \leftarrow \zeta_{\theta}+1
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Антенна().Тип антенны().Амплитудно-частотная характеристика(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega
) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ne 0}
- Вернуть Массив(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T )
Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta_{\varphi} (s_j,~\theta,~\varphi) = {\rm const}} , и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta_{\theta} (s_j,~\theta) = {\rm const}} , то есть углы распределены равномерно, таблица может быть реализована в виде массива значений Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)} , элементы которого могут заполняться параллельно, без синхронизации. Если же размер таблицы заранее не определен (общий случай), то таблица реализуется связанным списком, добавление элементов в который должно защищаться мьютексом на шаге 4.1.3.1.3.1.1, а алгоритм на заключительном шаге преобразует связанный список в массив с произвольным доступом. Второй путь при параллельном выполнении - создавать таблицы в локальной памяти потока, после выполнения которых - объединять таблицы в массив в основном потоке.
Параллельная форма
Параллельное выполнение в общем случае возможно только цикла, перебирающего первичные источники (шаг 4), так как распределение углов заранее не определено.
Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P>0} - число потоков, выполняющих функцию. Пусть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T'} - массив изначально пустых связанных списков троек Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)} , так, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle T'_{i}} - Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i -тый список массива, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 0\le i<P} .
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i \leftarrow} Номер итерации
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega \leftarrow Частота
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T'\leftarrow} Создать массив.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ s_j \in
G.Множество первичных источников()
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle t\leftarrow } индекс потока.
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j
.Антенна().Тип антенны().Амплитудно-частотная характеристика(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega
) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ne 0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\theta} \leftarrow 0
- Пока Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta < \pi
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi \leftarrow 0
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\varphi} \leftarrow 0
- Пока Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi<2\pi
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T'_t} .ДобавитьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle (s_j,~\theta,~\varphi)}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varphi \leftarrow \varphi + \frac{\Delta_{\varphi} (s_j,~\theta,~\varphi)}{2^i}}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\varphi} \leftarrow \zeta_{\varphi}+1
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle i=0 \vee \zeta_{\theta} \bmod 2 \neq 0 \vee \zeta_{\varphi} \bmod 2 \neq 0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta \leftarrow \theta + \frac{\Delta_{\theta} (s_j,~\theta)}{2^i}}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \zeta_{\theta} \leftarrow \zeta_{\theta}+1
- Вернуть МассивНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left(\bigsqcup_{t=0}^{P-1}T'_t\right)}
Trace
Функция трассирует луч через геометрическую модель и и фиксирует его прохождение вблизи контрольной точки.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R\leftarrow \infty
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T\leftarrow NaN
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ f_m\in
G.Множество отражающих объектов()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p \leftarrow Ray.Пересечение(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} .Плоскость())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn}
.Принадлежность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p
)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r\leftarrow Ray.Пробег(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p )
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r < R
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): R \leftarrow r
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T \leftarrow t_{mn}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow p
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ O_k \in
G.Множество плоскостей вывода результатов()
- Ray.Пересечение(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): O_k .Плоскость())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): O_k
.Принадлежность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p
)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r\leftarrow Ray.Пробег(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p )
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r < R
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): O_k .Ближайшая контрольная точка(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p )
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho .Зарегистрировать(Ray, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): r , G.Среда распространения())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T \not\equiv
NaN
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \gamma \leftarrow Ray.Угол пересечения(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T .Плоскость())
- Ray.Отразить(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T,~P,~R,~\gamma , G.Среда распространения())
- Если Ray.Напряженность Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): >E_{end}
- Trace(Ray, G, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E_{end} )
Postprocessing
Функция "проявляет" поле в контрольных точках по накопленным значениям напряженности от всех пришедших лучей.
SucApprox
Функция сравнивает текущие результаты моделирования с результатами, полученными на предыдущем шаге. На выходе получаем флаг, по которому решаем, следует ли продолжать уточнять модель.
Свойства алгоритма
Сложность
Возможности распараллеливания
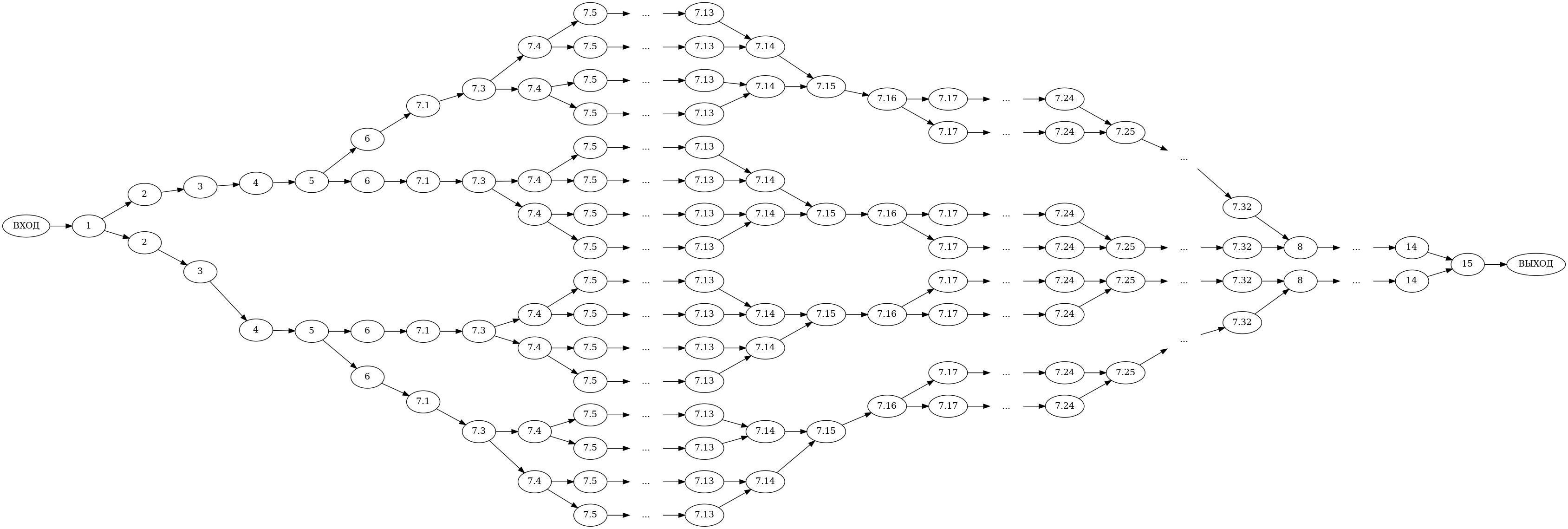
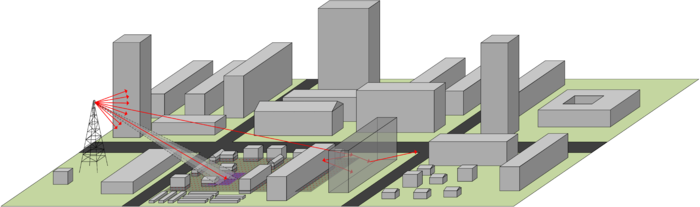
 по зениту источника являются функциями от направления либо постоянными.
по зениту источника являются функциями от направления либо постоянными.
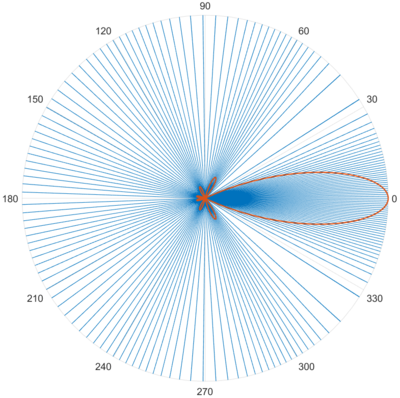
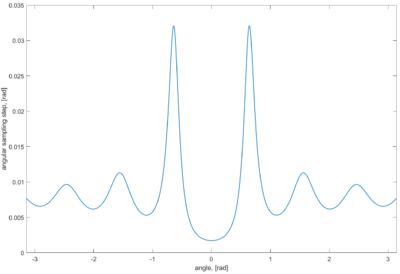
 - частота излучения;
- частота излучения; ,
,
 .
.


 ))
)) Расстояние(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P'
)
Расстояние(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P'
) Distance
Distance

 .Зарегистрировать(
.Зарегистрировать( , Расстояние(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k
.Позиция()),
, Расстояние(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k
.Позиция()),  )
)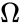 - список частот, на которых необходимо провести моделирование.
- список частот, на которых необходимо провести моделирование.


