Распространение радиоволн ВЧ/Метод зеркальных отображений: различия между версиями
Nigiluk (обсуждение | вклад) |
Nigiluk (обсуждение | вклад) |
||
| (не показана 21 промежуточная версия 2 участников) | |||
| Строка 1: | Строка 1: | ||
=Модель= | =Модель= | ||
[[Файл:Method of image charges.png|700px|thumb|right| | [[Файл:Method of image charges.png|700px|thumb|right|Канал Релея]] | ||
[[Файл:Image Source.png|300px|thumb|right|Паттерн мнимых источников]] | |||
Метод изображений (метод зеркальных отображений) широко применяется в электростатике и электродинамике для решения краевых задач. В частности, в приближении геометрической оптики данный метод позволяет построить картину хода лучей при любом числе отражений. | Метод изображений (метод зеркальных отображений) широко применяется в электростатике и электродинамике для решения краевых задач. В частности, в приближении геометрической оптики данный метод позволяет построить картину хода лучей при любом числе отражений. | ||
| Строка 8: | Строка 9: | ||
=Алгоритм= | =Алгоритм= | ||
==Предикат последнего отражения== | ==Инициализация функций== | ||
===Функция трассировки=== | |||
<tt>[Источник_2, B]=Tracing(I, Стек_точек, Стек_граней, Источник_1, Частота, G)</tt> | |||
#<math>S \leftarrow</math><tt> Источник_1</tt> | |||
#Пока <math>I>0</math> | |||
##<math>\rho \leftarrow</math><tt> Стек_точек</tt> | |||
##<math>t \leftarrow</math><tt> Стек_граней</tt> | |||
##<math>P \leftarrow</math><tt> <math>S</math>.Антенна().Позиция()</tt> | |||
##<math>Ray \leftarrow</math><tt> Луч().Создать(<math>P</math>, Вектор(<math>P</math>, <math>\rho</math>,1))</tt> | |||
##<math>p \leftarrow</math><tt> <math>Ray</math>.Пересечение(<math>t</math>.Плоскость грани())</tt> | |||
##Если <tt><math>t</math>.Принадлежность(<math>p</math>) <math>\wedge</math> Расстояние(<math>P,\rho</math>) <math>></math> Расстояние(<math>P,p</math>)</tt> <math>\wedge</math> НЕ <tt>IsShadowed(<math>Ray</math>, <math>p</math>, G)</tt> | |||
###<math>Angle \leftarrow</math><tt> <math>Ray</math>.Угол пересечения(<math>t</math>.Плоскость грани())</tt> | |||
###<math>S \leftarrow</math><tt> Вторичный источник при рейтрейсинге.Создать(<math>S</math>.Напряженность(Частота, <math>p</math>, G.Среда распространения), <math>Angle</math>, <math>p</math>, <math>t</math>)</tt> | |||
##Иначе | |||
###<math>B \leftarrow</math> ЛОЖЬ | |||
###ВЫХОД | |||
##<math>I \leftarrow I-1</math> | |||
#<tt> Источник_2 </tt><math>\leftarrow S</math> | |||
#<math>B \leftarrow</math> ИСТИНА | |||
#ВЫХОД | |||
===Рекурсия=== | |||
<tt>NewLevel(I, Стек_точек, Стек_граней, Источник_1, Контрольная_точка, Частота, G)</tt> | |||
#<tt><math>stack_{\rho} \leftarrow</math> Стек_точек</tt> | |||
#<tt><math>stack_t \leftarrow</math> Стек_граней</tt> | |||
#<tt><math>s \leftarrow</math> Источник_1</tt> | |||
#<tt><math>\omega \leftarrow</math> Частота</tt> | |||
#<tt><math>\Rho \leftarrow</math> Контрольная_точка</tt> | |||
#<math>I \leftarrow I+1</math> | |||
#<math>\forall ~ f_m\in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].Множество отражающих объектов()</tt> | |||
##<math>\forall ~ t_{mn} \in f_m</math><tt>.Множество отражающих поверхностей()</tt> | |||
###<math>\rho \Leftarrow stack_{\rho}</math> | |||
###<tt><math>\rho \leftarrow</math> [[Распространение радиоволн ВЧ/Точка|<math>\rho</math>]].Построить зеркальное отображение([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость грани())</tt> | |||
###<math>stack_{\rho} \leftarrow \rho</math> | |||
###<math>stack_t \leftarrow t_{mn}</math> | |||
###<tt><math>[S,~B] \leftarrow </math> Tracing(<math>I,~stack_{\rho},~stack_t,~s,~\omega,~</math> [[Распространение радиоволн ВЧ/Геометрическая модель|G]])</tt> | |||
###Если <math>B</math> | |||
####<tt><math>P \leftarrow</math> [[Распространение радиоволн ВЧ/Источник|<math>S</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].Позиция()</tt> | |||
####<tt><math>p \leftarrow</math> [[Распространение радиоволн ВЧ/Контрольная точка|<math>\Rho</math>]].Позиция()</tt> | |||
####<tt><math>Ray\leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Луч()]].Создать(<math>P</math>, Вектор(<math>P</math>, <math>p</math>, 1))</tt> | |||
####Если НЕ <tt>IsShadowed(<math>Ray,p,</math>[[Распространение радиоволн ВЧ/Геометрическая модель|G]])</tt> | |||
#####<tt><math>\Rho</math>.Зарегистрировать([[Распространение радиоволн ВЧ/Источник|<math>S</math>]].Напряженность(<math>\omega,~p</math>, [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]]))</tt> | |||
###Если НЕ <tt>IsEnd(<math>E,~I~,i</math>)</tt> | |||
####<tt>NewLevel(<math>I,~stack_{\rho},~stack_t,~s,~\Rho,~\omega,~</math> [[Распространение радиоволн ВЧ/Геометрическая модель|G]])</tt> | |||
###<math>\rho \leftarrow stack_{\rho}</math> | |||
###<math>t_{mn} \leftarrow stack_t</math> | |||
#ВЫХОД | |||
===Предикат последнего отражения=== | |||
<tt>IsEnd(E, I, i)</tt> | |||
В связи с тем, что количество элементарных модельных экспериментов, а следовательно и временные издержки алгоритма, зависит от числа отражающих поверхностей <math>T</math> и порядка отражения <math>I</math> как <math>N=T^I</math>, то важно определить максимальный существенный для текущих условий порядок переотражения сигнала. Введем предикат последнего отражения следующим образом: | В связи с тем, что количество элементарных модельных экспериментов, а следовательно и временные издержки алгоритма, зависит от числа отражающих поверхностей <math>T</math> и порядка отражения <math>I</math> как <math>N=T^I</math>, то важно определить максимальный существенный для текущих условий порядок переотражения сигнала. Введем предикат последнего отражения следующим образом: | ||
| Строка 21: | Строка 74: | ||
::<math>I',I </math> - порядки переотражения, при которых сигнал пришел в контрольную точку | ::<math>I',I </math> - порядки переотражения, при которых сигнал пришел в контрольную точку | ||
Таким образом данный предикат имеет следующий вид < | Таким образом данный предикат имеет следующий вид <tt>IsEnd(E, I, i)</tt><math>=1 \vee 2 \vee 3</math> | ||
===Предикат тени=== | |||
<tt>IsShadowed(Луч, Точка, G)</tt> | |||
Данный предикат проверяет наличие препятствия на пути <tt>[[Распространение радиоволн ВЧ/Луч|Луча]]</tt> в некоторую [[Распространение радиоволн ВЧ/Точка|точку]] P путем проверки нахождения отражающих объектов из множества G.Множество отражающих объектов(), где G - геометрическая модель, на отрезке Луч.Позиция() - P, исключая поверхности, на которых лежат P и Луч.Позиция(), если такие отражающие поверхности существуют. | |||
#<tt><math>P \leftarrow</math> Точка</tt> | |||
#<math>\forall ~ f_m\in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].Множество отражающих объектов()</tt> | |||
##<math>\forall ~ t_{mn} \in f_m</math><tt>.Множество отражающих поверхностей()</tt> | |||
###<tt><math>P'\leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Луч]].Пересечение([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость грани())</tt> | |||
###Если <tt>[[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Принадлежность(<math>P'</math>) <math>\wedge</math> Расстояние([[Распространение радиоволн ВЧ/Луч|Луч]].Позиция(),<math>P</math>) <math>></math> Расстояние( Расстояние([[Распространение радиоволн ВЧ/Луч|Луч]].Позиция(),<math>P'</math>)</tt> | |||
#### Вернуть ИСТИНА | |||
# Вернуть ЛОЖЬ | |||
==Предусловия== | ==Предусловия== | ||
<math>stack_{t}</math> - аналог стековой памяти, хранящей информацию о занесенных в нее отражающих поверхностей | <math>stack_{t}</math> - аналог стековой памяти, хранящей информацию о занесенных в нее отражающих поверхностей | ||
:<math>stack_{t}=\begin{Bmatrix} | :<math>stack_{t}=\begin{Bmatrix} t&t&\cdots&t \end{Bmatrix}</math>, где | ||
:<math> | :<math>t</math> хранятся в виде ссылок на соответствующие элементы. | ||
<math>stack_{\rho}</math> - аналог стековой памяти, хранящей информацию о занесенных в нее | <math>stack_{\rho}</math> - аналог стековой памяти, хранящей информацию о занесенных в нее мнимых [[Распространение радиоволн ВЧ/Точка|точках]] | ||
:<math>stack_{\rho}=\begin{Bmatrix} \rho&\rho&\cdots&\rho \end{Bmatrix}</math> | :<math>stack_{\rho}=\begin{Bmatrix} \rho&\rho&\cdots&\rho \end{Bmatrix}</math> | ||
Операции <math>stack \leftarrow x</math> и <math>x \leftarrow stack</math> аналогичны операциям push и pop соответственно | Операции <math>stack \leftarrow x</math> и <math>x \leftarrow stack</math> аналогичны операциям push и pop соответственно. Операция <math>x \Leftarrow stack</math> копирует последний элемент стека в x без извлечения. | ||
<math>stack_t',stack_{\rho}'</math> - локальные переменные, аналогичные <math>stack_t,stack_{\rho}</math>, использующиеся во внутренних подциклах | <math>stack_t',stack_{\rho}'</math> - локальные переменные, аналогичные <math>stack_t,stack_{\rho}</math>, использующиеся во внутренних подциклах | ||
| Строка 57: | Строка 121: | ||
#####<math>t_{mn} \leftarrow stack_{t}'</math> | #####<math>t_{mn} \leftarrow stack_{t}'</math> | ||
#####Ray <math>\leftarrow</math><tt> [[Распространение радиоволн ВЧ/Луч|Луч()]].Создать(Position, Вектор(Position,[[Распространение радиоволн ВЧ/Контрольная точка|<math>\rho'</math>]].Позиция(), 1))</tt> | #####Ray <math>\leftarrow</math><tt> [[Распространение радиоволн ВЧ/Луч|Луч()]].Создать(Position, Вектор(Position,[[Распространение радиоволн ВЧ/Контрольная точка|<math>\rho'</math>]].Позиция(), 1))</tt> | ||
#####Если <math>I' > 0</math> | #####Если <math>I' > 0</math> | ||
######<tt><math>P\leftarrow</math>[[Распространение радиоволн ВЧ/Луч|Ray]].Пересечение([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость грани())</tt> | ######<tt><math>P\leftarrow</math>[[Распространение радиоволн ВЧ/Луч|Ray]].Пересечение([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость грани())</tt> | ||
######Если <tt>[[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Принадлежность(<math>P</math>) <math>\wedge</math> Расстояние(Position,<math>\rho'</math>.Позиция()) <math>></math> Расстояние(Position,<math>P</math>)</tt> | ######Если <tt>[[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Принадлежность(<math>P</math>) <math>\wedge</math> Расстояние(Position,<math>\rho'</math>.Позиция()) <math>></math> Расстояние(Position,<math>P</math>)</tt> | ||
| Строка 65: | Строка 127: | ||
######Иначе | ######Иначе | ||
#######Переход 1.1.8.1.14 | #######Переход 1.1.8.1.14 | ||
##### | #####Иначе | ||
######<math>\ | ######<math>P\leftarrow</math><tt>[[Распространение радиоволн ВЧ/Контрольная точка|<math>\rho'</math>]].Позиция()</tt> | ||
#####Если <tt>IsShadowed(Ray, P, G)</tt> | |||
######Переход 1.1.8.1.14 | |||
#####Если <math>I' > 0</math> | #####Если <math>I' > 0</math> | ||
######Angle <tt><math>\leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Угол пересечения([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость грани())</tt> | ######Angle <tt><math>\leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Ray]].Угол пересечения([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость грани())</tt> | ||
| Строка 76: | Строка 137: | ||
######<math>I' \leftarrow I'-1</math> | ######<math>I' \leftarrow I'-1</math> | ||
######Переход 1.1.8.5 | ######Переход 1.1.8.5 | ||
#####<tt><math>\ | #####<tt><math>\rho'</math>.Зарегистрировать([[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].Напряженность<math>(\omega_n,~\theta,~\varphi</math>, Расстояние(Position, <math>\rho'</math>.Позиция()), [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]]<math>)</math>)</tt> | ||
#####Если <math>E > E_{end}</math> {{mark|text=См. обсуждение к статье.}} | #####Если <math>E > E_{end}</math> {{mark|text=См. обсуждение к статье.}} | ||
######<math>I \leftarrow I+1</math> | ######<math>I \leftarrow I+1</math> | ||
| Строка 82: | Строка 143: | ||
######<math>stack_{\rho} \leftarrow \rho'</math> | ######<math>stack_{\rho} \leftarrow \rho'</math> | ||
######Переход 1.1.6 | ######Переход 1.1.6 | ||
###<math>I \leftarrow I-1</math> | |||
###Если <math>I > 0</math> | |||
####<math>t_{m,n} \leftarrow stack_t</math> | |||
####<math>\rho' \leftarrow stack_{\rho}</math> | |||
####Переход 1.1.8 | |||
###<math>s_j \leftarrow s'</math> | ###<math>s_j \leftarrow s'</math> | ||
#<math>\forall ~ \rho_k \in </math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Множество контрольных точек|Множество контрольных точек()]]</tt> | |||
##<tt><math>\forall ~ s_j \in</math> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].Множество первичных источников()</tt> | |||
###<math>\forall ~ \omega_n \in</math><tt> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].[[Распространение радиоволн ВЧ/Тип антенны|Тип антенны()]].[[Распространение радиоволн ВЧ/Амплитудно-частотная характеристика|Амплитудно-частотная характеристика()]]</tt> | |||
####<tt><math>P \leftarrow</math> [[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].Позиция()</tt> | |||
####<tt><math>p \leftarrow</math> [[Распространение радиоволн ВЧ/Контрольная точка|<math>\rho_k</math>]].Позиция()</tt> | |||
####<tt><math>Ray\leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Луч()]].Создать(<math>P</math>, Вектор(<math>P</math>, <math>p</math>, 1))</tt> | |||
####Если НЕ <tt>IsShadowed(<math>Ray,p,</math>[[Распространение радиоволн ВЧ/Геометрическая модель|G]])</tt> | |||
#####<tt><math>\rho_k</math>.Зарегистрировать([[Распространение радиоволн ВЧ/Источник|<math>s_j</math>]].Напряженность(<math>\omega_n,~p</math>, [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]]))</tt> | |||
####<math>I \leftarrow 1</math> | |||
####<math>\forall ~ f_m\in</math><tt> [[Распространение радиоволн ВЧ/Геометрическая модель|G]].Множество отражающих объектов()</tt> | |||
#####<math>\forall ~ t_{mn} \in f_m</math><tt>.Множество отражающих поверхностей()</tt> | |||
######<tt><math>\rho \leftarrow</math> [[Распространение радиоволн ВЧ/Контрольная точка|<math>\rho_k</math>]].Построить зеркальное отображение([[Распространение радиоволн ВЧ/Грань отражающего объекта|<math>t_{mn}</math>]].Плоскость грани())</tt> | |||
######<math>stack_{\rho} \leftarrow \rho</math> | |||
######<math>stack_t \leftarrow t_{mn}</math> | |||
######<tt><math>[S,~B] \leftarrow </math> Tracing(<math>I,~stack_{\rho},~stack_t,~s_j,~\omega_n,~</math> [[Распространение радиоволн ВЧ/Геометрическая модель|G]])</tt> | |||
######Если <math>B</math> | |||
#######<tt><math>P \leftarrow</math> [[Распространение радиоволн ВЧ/Источник|<math>S</math>]].[[Распространение радиоволн ВЧ/Антенна|Антенна()]].Позиция()</tt> | |||
#######<tt><math>p \leftarrow</math> [[Распространение радиоволн ВЧ/Контрольная точка|<math>\rho_k</math>]].Позиция()</tt> | |||
#######<tt><math>Ray\leftarrow</math> [[Распространение радиоволн ВЧ/Луч|Луч()]].Создать(<math>P</math>, Вектор(<math>P</math>, <math>p</math>, 1))</tt> | |||
#######Если НЕ <tt>IsShadowed(<math>Ray,p,</math>[[Распространение радиоволн ВЧ/Геометрическая модель|G]])</tt> | |||
########<tt><math>\rho_k</math>.Зарегистрировать([[Распространение радиоволн ВЧ/Источник|<math>S</math>]].Напряженность(<math>\omega_n,~p</math>, [[Распространение радиоволн ВЧ/Геометрическая модель|G]].[[Распространение радиоволн ВЧ/Среда распространения|Среда распространения()]]))</tt> | |||
######Если НЕ <tt>IsEnd(<math>E,~I~,i</math>)</tt> | |||
#######<tt>NewLevel(<math>I,~stack_{\rho},~stack_t,~s_j,~\rho_k,~\omega_n,~</math> [[Распространение радиоволн ВЧ/Геометрическая модель|G]])</tt> | |||
######<math>\rho \leftarrow stack_{\rho}</math> | |||
######<math>t_{mn} \leftarrow stack_t</math> | |||
====Возможности распараллеливания==== | |||
<graphviz size=500px> | |||
digraph image_source_EM_parallel_run{ | |||
rankdir=TB; | |||
node[fontsize=14]; | |||
edge[fontsize=14]; | |||
G0[label="ВХОД"]; | |||
G1[label="1"]; | |||
G2_1[label="2"]; | |||
G2_2[label="2"]; | |||
G3_1_1[label="3"]; | |||
G3_1_2[label="3"]; | |||
G3_2_1[label="3"]; | |||
G3_2_2[label="3"]; | |||
G4_1_1_1[label="4"]; | |||
G4_1_1_2[label="4"]; | |||
G4_1_2_1[label="4"]; | |||
G4_1_2_2[label="4"]; | |||
G4_2_1_1[label="4"]; | |||
G4_2_1_2[label="4"]; | |||
G4_2_2_1[label="4"]; | |||
G4_2_2_2[label="4"]; | |||
SKIP1_1_1_1[label="...", shape="none"]; | |||
SKIP1_1_1_2[label="...", shape="none"]; | |||
SKIP1_1_2_1[label="...", shape="none"]; | |||
SKIP1_1_2_2[label="...", shape="none"]; | |||
SKIP1_2_1_1[label="...", shape="none"]; | |||
SKIP1_2_1_2[label="...", shape="none"]; | |||
SKIP1_2_2_1[label="...", shape="none"]; | |||
SKIP1_2_2_2[label="...", shape="none"]; | |||
G11_1_1_1[label="11"]; | |||
G11_1_1_2[label="11"]; | |||
G11_1_2_1[label="11"]; | |||
G11_1_2_2[label="11"]; | |||
G11_2_1_1[label="11"]; | |||
G11_2_1_2[label="11"]; | |||
G11_2_2_1[label="11"]; | |||
G11_2_2_2[label="11"]; | |||
G12_1_1_1_1[label="12"]; | |||
G12_1_1_1_2[label="12"]; | |||
G12_1_1_2_1[label="12"]; | |||
G12_1_1_2_2[label="12"]; | |||
G12_1_2_1_1[label="12"]; | |||
G12_1_2_1_2[label="12"]; | |||
G12_1_2_2_1[label="12"]; | |||
G12_1_2_2_2[label="12"]; | |||
G12_2_1_1_1[label="12"]; | |||
G12_2_1_1_2[label="12"]; | |||
G12_2_1_2_1[label="12"]; | |||
G12_2_1_2_2[label="12"]; | |||
G12_2_2_1_1[label="12"]; | |||
G12_2_2_1_2[label="12"]; | |||
G12_2_2_2_1[label="12"]; | |||
G12_2_2_2_2[label="12"]; | |||
G13_1_1_1_1_1[label="13"]; | |||
G13_1_1_1_1_2[label="13"]; | |||
G13_1_1_1_2_1[label="13"]; | |||
G13_1_1_1_2_2[label="13"]; | |||
G13_1_1_2_1_1[label="13"]; | |||
G13_1_1_2_1_2[label="13"]; | |||
G13_1_1_2_2_1[label="13"]; | |||
G13_1_1_2_2_2[label="13"]; | |||
G13_1_2_1_1_1[label="13"]; | |||
G13_1_2_1_1_2[label="13"]; | |||
G13_1_2_1_2_1[label="13"]; | |||
G13_1_2_1_2_2[label="13"]; | |||
G13_1_2_2_1_1[label="13"]; | |||
G13_1_2_2_1_2[label="13"]; | |||
G13_1_2_2_2_1[label="13"]; | |||
G13_1_2_2_2_2[label="13"]; | |||
G13_2_1_1_1_1[label="13"]; | |||
G13_2_1_1_1_2[label="13"]; | |||
G13_2_1_1_2_1[label="13"]; | |||
G13_2_1_1_2_2[label="13"]; | |||
G13_2_1_2_1_1[label="13"]; | |||
G13_2_1_2_1_2[label="13"]; | |||
G13_2_1_2_2_1[label="13"]; | |||
G13_2_1_2_2_2[label="13"]; | |||
G13_2_2_1_1_1[label="13"]; | |||
G13_2_2_1_1_2[label="13"]; | |||
G13_2_2_1_2_1[label="13"]; | |||
G13_2_2_1_2_2[label="13"]; | |||
G13_2_2_2_1_1[label="13"]; | |||
G13_2_2_2_1_2[label="13"]; | |||
G13_2_2_2_2_1[label="13"]; | |||
G13_2_2_2_2_2[label="13"]; | |||
SKIP2_1_1_1_1_1[label="...", shape="none"]; | |||
SKIP2_1_1_1_1_2[label="...", shape="none"]; | |||
SKIP2_1_1_1_2_1[label="...", shape="none"]; | |||
SKIP2_1_1_1_2_2[label="...", shape="none"]; | |||
SKIP2_1_1_2_1_1[label="...", shape="none"]; | |||
SKIP2_1_1_2_1_2[label="...", shape="none"]; | |||
SKIP2_1_1_2_2_1[label="...", shape="none"]; | |||
SKIP2_1_1_2_2_2[label="...", shape="none"]; | |||
SKIP2_1_2_1_1_1[label="...", shape="none"]; | |||
SKIP2_1_2_1_1_2[label="...", shape="none"]; | |||
SKIP2_1_2_1_2_1[label="...", shape="none"]; | |||
SKIP2_1_2_1_2_2[label="...", shape="none"]; | |||
SKIP2_1_2_2_1_1[label="...", shape="none"]; | |||
SKIP2_1_2_2_1_2[label="...", shape="none"]; | |||
SKIP2_1_2_2_2_1[label="...", shape="none"]; | |||
SKIP2_1_2_2_2_2[label="...", shape="none"]; | |||
SKIP2_2_1_1_1_1[label="...", shape="none"]; | |||
SKIP2_2_1_1_1_2[label="...", shape="none"]; | |||
SKIP2_2_1_1_2_1[label="...", shape="none"]; | |||
SKIP2_2_1_1_2_2[label="...", shape="none"]; | |||
SKIP2_2_1_2_1_1[label="...", shape="none"]; | |||
SKIP2_2_1_2_1_2[label="...", shape="none"]; | |||
SKIP2_2_1_2_2_1[label="...", shape="none"]; | |||
SKIP2_2_1_2_2_2[label="...", shape="none"]; | |||
SKIP2_2_2_1_1_1[label="...", shape="none"]; | |||
SKIP2_2_2_1_1_2[label="...", shape="none"]; | |||
SKIP2_2_2_1_2_1[label="...", shape="none"]; | |||
SKIP2_2_2_1_2_2[label="...", shape="none"]; | |||
SKIP2_2_2_2_1_1[label="...", shape="none"]; | |||
SKIP2_2_2_2_1_2[label="...", shape="none"]; | |||
SKIP2_2_2_2_2_1[label="...", shape="none"]; | |||
SKIP2_2_2_2_2_2[label="...", shape="none"]; | |||
G29_1_1_1_1_1[label="29"]; | |||
G29_1_1_1_1_2[label="29"]; | |||
G29_1_1_1_2_1[label="29"]; | |||
G29_1_1_1_2_2[label="29"]; | |||
G29_1_1_2_1_1[label="29"]; | |||
G29_1_1_2_1_2[label="29"]; | |||
G29_1_1_2_2_1[label="29"]; | |||
G29_1_1_2_2_2[label="29"]; | |||
G29_1_2_1_1_1[label="29"]; | |||
G29_1_2_1_1_2[label="29"]; | |||
G29_1_2_1_2_1[label="29"]; | |||
G29_1_2_1_2_2[label="29"]; | |||
G29_1_2_2_1_1[label="29"]; | |||
G29_1_2_2_1_2[label="29"]; | |||
G29_1_2_2_2_1[label="29"]; | |||
G29_1_2_2_2_2[label="29"]; | |||
G29_2_1_1_1_1[label="29"]; | |||
G29_2_1_1_1_2[label="29"]; | |||
G29_2_1_1_2_1[label="29"]; | |||
G29_2_1_1_2_2[label="29"]; | |||
G29_2_1_2_1_1[label="29"]; | |||
G29_2_1_2_1_2[label="29"]; | |||
G29_2_1_2_2_1[label="29"]; | |||
G29_2_1_2_2_2[label="29"]; | |||
G29_2_2_1_1_1[label="29"]; | |||
G29_2_2_1_1_2[label="29"]; | |||
G29_2_2_1_2_1[label="29"]; | |||
G29_2_2_1_2_2[label="29"]; | |||
G29_2_2_2_1_1[label="29"]; | |||
G29_2_2_2_1_2[label="29"]; | |||
G29_2_2_2_2_1[label="29"]; | |||
G29_2_2_2_2_2[label="29"]; | |||
G30_1_1_1_1[label="30"]; | |||
G30_1_1_1_2[label="30"]; | |||
G30_1_1_2_1[label="30"]; | |||
G30_1_1_2_2[label="30"]; | |||
G30_1_2_1_1[label="30"]; | |||
G30_1_2_1_2[label="30"]; | |||
G30_1_2_2_1[label="30"]; | |||
G30_1_2_2_2[label="30"]; | |||
G30_2_1_1_1[label="30"]; | |||
G30_2_1_1_2[label="30"]; | |||
G30_2_1_2_1[label="30"]; | |||
G30_2_1_2_2[label="30"]; | |||
G30_2_2_1_1[label="30"]; | |||
G30_2_2_1_2[label="30"]; | |||
G30_2_2_2_1[label="30"]; | |||
G30_2_2_2_2[label="30"]; | |||
G31_1_1_1[label="31"]; | |||
G31_1_1_2[label="31"]; | |||
G31_1_2_1[label="31"]; | |||
G31_1_2_2[label="31"]; | |||
G31_2_1_1[label="31"]; | |||
G31_2_1_2[label="31"]; | |||
G31_2_2_1[label="31"]; | |||
G31_2_2_2[label="31"]; | |||
G32_1_1[label="32"]; | |||
G32_1_2[label="32"]; | |||
G32_2_1[label="32"]; | |||
G32_2_2[label="32"]; | |||
G33_1[label="33"]; | |||
G33_2[label="33"]; | |||
G34[label="34"]; | |||
G35[label="ВЫХОД"]; | |||
G0->G1->{G2_1; G2_2} | |||
G2_1->{G3_1_1; G3_1_2} | |||
G2_2->{G3_2_1; G3_2_2} | |||
G3_1_1->{G4_1_1_1; G4_1_1_2} | |||
G3_1_2->{G4_1_2_1; G4_1_2_2} | |||
G3_2_1->{G4_2_1_1; G4_2_1_2} | |||
G3_2_2->{G4_2_2_1; G4_2_2_2} | |||
G4_1_1_1->SKIP1_1_1_1->G11_1_1_1->{G12_1_1_1_1; G12_1_1_1_2} | |||
G4_1_1_2->SKIP1_1_1_2->G11_1_1_2->{G12_1_1_2_1; G12_1_1_2_2} | |||
G4_1_2_1->SKIP1_1_2_1->G11_1_2_1->{G12_1_2_1_1; G12_1_2_1_2} | |||
G4_1_2_2->SKIP1_1_2_2->G11_1_2_2->{G12_1_2_2_1; G12_1_2_2_2} | |||
G4_2_1_1->SKIP1_2_1_1->G11_2_1_1->{G12_2_1_1_1; G12_2_1_1_2} | |||
G4_2_1_2->SKIP1_2_1_2->G11_2_1_2->{G12_2_1_2_1; G12_2_1_2_2} | |||
G4_2_2_1->SKIP1_2_2_1->G11_2_2_1->{G12_2_2_1_1; G12_2_2_1_2} | |||
G4_2_2_2->SKIP1_2_2_2->G11_2_2_2->{G12_2_2_2_1; G12_2_2_2_2} | |||
G12_1_1_1_1->{G13_1_1_1_1_1; G13_1_1_1_1_2} | |||
G12_1_1_1_2->{G13_1_1_1_2_1; G13_1_1_1_2_2} | |||
G12_1_1_2_1->{G13_1_1_2_1_1; G13_1_1_2_1_2} | |||
G12_1_1_2_2->{G13_1_1_2_2_1; G13_1_1_2_2_2} | |||
G12_1_2_1_1->{G13_1_2_1_1_1; G13_1_2_1_1_2} | |||
G12_1_2_1_2->{G13_1_2_1_2_1; G13_1_2_1_2_2} | |||
G12_1_2_2_1->{G13_1_2_2_1_1; G13_1_2_2_1_2} | |||
G12_1_2_2_2->{G13_1_2_2_2_1; G13_1_2_2_2_2} | |||
G12_2_1_1_1->{G13_2_1_1_1_1; G13_2_1_1_1_2} | |||
G12_2_1_1_2->{G13_2_1_1_2_1; G13_2_1_1_2_2} | |||
G12_2_1_2_1->{G13_2_1_2_1_1; G13_2_1_2_1_2} | |||
G12_2_1_2_2->{G13_2_1_2_2_1; G13_2_1_2_2_2} | |||
G12_2_2_1_1->{G13_2_2_1_1_1; G13_2_2_1_1_2} | |||
G12_2_2_1_2->{G13_2_2_1_2_1; G13_2_2_1_2_2} | |||
G12_2_2_2_1->{G13_2_2_2_1_1; G13_2_2_2_1_2} | |||
G12_2_2_2_2->{G13_2_2_2_2_1; G13_2_2_2_2_2} | |||
G13_1_1_1_1_1->SKIP2_1_1_1_1_1->G29_1_1_1_1_1 | |||
G13_1_1_1_1_2->SKIP2_1_1_1_1_2->G29_1_1_1_1_2 | |||
G13_1_1_1_2_1->SKIP2_1_1_1_2_1->G29_1_1_1_2_1 | |||
G13_1_1_1_2_2->SKIP2_1_1_1_2_2->G29_1_1_1_2_2 | |||
G13_1_1_2_1_1->SKIP2_1_1_2_1_1->G29_1_1_2_1_1 | |||
G13_1_1_2_1_2->SKIP2_1_1_2_1_2->G29_1_1_2_1_2 | |||
G13_1_1_2_2_1->SKIP2_1_1_2_2_1->G29_1_1_2_2_1 | |||
G13_1_1_2_2_2->SKIP2_1_1_2_2_2->G29_1_1_2_2_2 | |||
G13_1_2_1_1_1->SKIP2_1_2_1_1_1->G29_1_2_1_1_1 | |||
G13_1_2_1_1_2->SKIP2_1_2_1_1_2->G29_1_2_1_1_2 | |||
G13_1_2_1_2_1->SKIP2_1_2_1_2_1->G29_1_2_1_2_1 | |||
G13_1_2_1_2_2->SKIP2_1_2_1_2_2->G29_1_2_1_2_2 | |||
G13_1_2_2_1_1->SKIP2_1_2_2_1_1->G29_1_2_2_1_1 | |||
G13_1_2_2_1_2->SKIP2_1_2_2_1_2->G29_1_2_2_1_2 | |||
G13_1_2_2_2_1->SKIP2_1_2_2_2_1->G29_1_2_2_2_1 | |||
G13_1_2_2_2_2->SKIP2_1_2_2_2_2->G29_1_2_2_2_2 | |||
G13_2_1_1_1_1->SKIP2_2_1_1_1_1->G29_2_1_1_1_1 | |||
G13_2_1_1_1_2->SKIP2_2_1_1_1_2->G29_2_1_1_1_2 | |||
G13_2_1_1_2_1->SKIP2_2_1_1_2_1->G29_2_1_1_2_1 | |||
G13_2_1_1_2_2->SKIP2_2_1_1_2_2->G29_2_1_1_2_2 | |||
G13_2_1_2_1_1->SKIP2_2_1_2_1_1->G29_2_1_2_1_1 | |||
G13_2_1_2_1_2->SKIP2_2_1_2_1_2->G29_2_1_2_1_2 | |||
G13_2_1_2_2_1->SKIP2_2_1_2_2_1->G29_2_1_2_2_1 | |||
G13_2_1_2_2_2->SKIP2_2_1_2_2_2->G29_2_1_2_2_2 | |||
G13_2_2_1_1_1->SKIP2_2_2_1_1_1->G29_2_2_1_1_1 | |||
G13_2_2_1_1_2->SKIP2_2_2_1_1_2->G29_2_2_1_1_2 | |||
G13_2_2_1_2_1->SKIP2_2_2_1_2_1->G29_2_2_1_2_1 | |||
G13_2_2_1_2_2->SKIP2_2_2_1_2_2->G29_2_2_1_2_2 | |||
G13_2_2_2_1_1->SKIP2_2_2_2_1_1->G29_2_2_2_1_1 | |||
G13_2_2_2_1_2->SKIP2_2_2_2_1_2->G29_2_2_2_1_2 | |||
G13_2_2_2_2_1->SKIP2_2_2_2_2_1->G29_2_2_2_2_1 | |||
G13_2_2_2_2_2->SKIP2_2_2_2_2_2->G29_2_2_2_2_2 | |||
{G29_1_1_1_1_1; G29_1_1_1_1_2}->G30_1_1_1_1 | |||
{G29_1_1_1_2_1; G29_1_1_1_2_2}->G30_1_1_1_2 | |||
{G29_1_1_2_1_1; G29_1_1_2_1_2}->G30_1_1_2_1 | |||
{G29_1_1_2_2_1; G29_1_1_2_2_2}->G30_1_1_2_2 | |||
{G29_1_2_1_1_1; G29_1_2_1_1_2}->G30_1_2_1_1 | |||
{G29_1_2_1_2_1; G29_1_2_1_2_2}->G30_1_2_1_2 | |||
{G29_1_2_2_1_1; G29_1_2_2_1_2}->G30_1_2_2_1 | |||
{G29_1_2_2_2_1; G29_1_2_2_2_2}->G30_1_2_2_2 | |||
{G29_2_1_1_1_1; G29_2_1_1_1_2}->G30_2_1_1_1 | |||
{G29_2_1_1_2_1; G29_2_1_1_2_2}->G30_2_1_1_2 | |||
{G29_2_1_2_1_1; G29_2_1_2_1_2}->G30_2_1_2_1 | |||
{G29_2_1_2_2_1; G29_2_1_2_2_2}->G30_2_1_2_2 | |||
{G29_2_2_1_1_1; G29_2_2_1_1_2}->G30_2_2_1_1 | |||
{G29_2_2_1_2_1; G29_2_2_1_2_2}->G30_2_2_1_2 | |||
{G29_2_2_2_1_1; G29_2_2_2_1_2}->G30_2_2_2_1 | |||
{G29_2_2_2_2_1; G29_2_2_2_2_2}->G30_2_2_2_2 | |||
{G30_1_1_1_1; G30_1_1_1_2}->G31_1_1_1 | |||
{G30_1_1_2_1; G30_1_1_2_2}->G31_1_1_2 | |||
{G30_1_2_1_1; G30_1_2_1_2}->G31_1_2_1 | |||
{G30_1_2_2_1; G30_1_2_2_2}->G31_1_2_2 | |||
{G30_2_1_1_1; G30_2_1_1_2}->G31_2_1_1 | |||
{G30_2_1_2_1; G30_2_1_2_2}->G31_2_1_2 | |||
{G30_2_2_1_1; G30_2_2_1_2}->G31_2_2_1 | |||
{G30_2_2_2_1; G30_2_2_2_2}->G31_2_2_2 | |||
{G31_1_1_1; G31_1_1_2}->G32_1_1 | |||
{G31_1_2_1; G31_1_2_2}->G32_1_2 | |||
{G31_2_1_1; G31_2_1_2}->G32_2_1 | |||
{G31_2_2_1; G31_2_2_2}->G32_2_2 | |||
{G32_1_1; G32_1_2}->G33_1 | |||
{G32_2_1; G32_2_2}->G33_2 | |||
{G33_1; G33_2}->G34->G35 | |||
} | |||
</graphviz> | |||
Текущая версия на 02:24, 21 июня 2017
Модель
Метод изображений (метод зеркальных отображений) широко применяется в электростатике и электродинамике для решения краевых задач. В частности, в приближении геометрической оптики данный метод позволяет построить картину хода лучей при любом числе отражений.
Суть метода состоит в построении лучей относительно мнимых изображений источника или приемника сигнала. Мнимые изображении строятся согласно правилам построения изображений в системе зеркал, здесь зеркала повторяют форму граничных поверхностей.
На рисунке представлена типичная ситуация в условиях плотной городской застройки, когда антенна приемного устройства находится в области геометрической тени относительно источника сигнала. Сигнал на приемной антенне является результатом переотражения радиоволны от внешней границы зданий, т.н. канал Релея. Зная координаты источника и приемника можно провести точную трассировку лучей с помощью простых геометрических построений.
Алгоритм
Инициализация функций
Функция трассировки
[Источник_2, B]=Tracing(I, Стек_точек, Стек_граней, Источник_1, Частота, G)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \leftarrow Источник_1
- Пока Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I>0
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho \leftarrow Стек_точек
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t \leftarrow Стек_граней
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S .Антенна().Позиция()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Ray \leftarrow Луч().Создать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P , Вектор(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho ,1))
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Ray .Пересечение(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t .Плоскость грани())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t
.Принадлежность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p
) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \wedge
Расстояние(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P,\rho
) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): >
Расстояние(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P,p
) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \wedge
НЕ IsShadowed(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Ray
, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p
, G)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Angle \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Ray .Угол пересечения(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t .Плоскость грани())
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S \leftarrow Вторичный источник при рейтрейсинге.Создать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S .Напряженность(Частота, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p , G.Среда распространения), Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Angle , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t )
- Иначе
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): B \leftarrow ЛОЖЬ
- ВЫХОД
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I \leftarrow I-1
- Источник_2 Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow S
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): B \leftarrow ИСТИНА
- ВЫХОД
Рекурсия
NewLevel(I, Стек_точек, Стек_граней, Источник_1, Контрольная_точка, Частота, G)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{\rho} \leftarrow Стек_точек
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_t \leftarrow Стек_граней
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s \leftarrow Источник_1
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega \leftarrow Частота
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Rho \leftarrow Контрольная_точка
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I \leftarrow I+1
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ f_m\in
G.Множество отражающих объектов()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho \Leftarrow stack_{\rho}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho .Построить зеркальное отображение(.Плоскость грани())
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{\rho} \leftarrow \rho
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_t \leftarrow t_{mn}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): [S,~B] \leftarrow Tracing(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I,~stack_{\rho},~stack_t,~s,~\omega,~ G)
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): B
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S .Антенна().Позиция()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Rho .Позиция()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Ray\leftarrow Луч().Создать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P , Вектор(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p , 1))
- Если НЕ IsShadowed(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Ray,p,
G)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \Rho .Зарегистрировать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S .Напряженность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega,~p , G.Среда распространения()))
- Если НЕ IsEnd()
- NewLevel(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I,~stack_{\rho},~stack_t,~s,~\Rho,~\omega,~ G)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho \leftarrow stack_{\rho}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} \leftarrow stack_t
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- ВЫХОД
Предикат последнего отражения
IsEnd(E, I, i)
В связи с тем, что количество элементарных модельных экспериментов, а следовательно и временные издержки алгоритма, зависит от числа отражающих поверхностей Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): T и порядка отражения Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I как Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): N=T^I , то важно определить максимальный существенный для текущих условий порядок переотражения сигнала. Введем предикат последнего отражения следующим образом:
1. Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E < E_{end} , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E_{end} - пренебрежимый уровень сигнала
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E = Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Напряженность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_n , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho' .Позиция(), G.Среда распространения())
2. Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I > I_{max} , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I_{max} - жестко ограниченный пользователем порядок переотражения
3. Если
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i_{max} - ограниченное пользователем максимальное число раз неприхода сигнала подряд
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): i = I' - I
, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I',I - порядки переотражения, при которых сигнал пришел в контрольную точку
Таким образом данный предикат имеет следующий вид IsEnd(E, I, i)Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): =1 \vee 2 \vee 3
Предикат тени
IsShadowed(Луч, Точка, G)
Данный предикат проверяет наличие препятствия на пути Луча в некоторую точку P путем проверки нахождения отражающих объектов из множества G.Множество отражающих объектов(), где G - геометрическая модель, на отрезке Луч.Позиция() - P, исключая поверхности, на которых лежат P и Луч.Позиция(), если такие отражающие поверхности существуют.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow Точка
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ f_m\in
G.Множество отражающих объектов()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P'\leftarrow Луч.Пересечение(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} .Плоскость грани())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn}
.Принадлежность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P'
) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \wedge
Расстояние(Луч.Позиция(),Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P
) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): >
Расстояние( Расстояние(Луч.Позиция(),Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P'
)
- Вернуть ИСТИНА
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Вернуть ЛОЖЬ
Предусловия
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{t} - аналог стековой памяти, хранящей информацию о занесенных в нее отражающих поверхностей
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{t}=\begin{Bmatrix} t&t&\cdots&t \end{Bmatrix} , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t хранятся в виде ссылок на соответствующие элементы.
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{\rho} - аналог стековой памяти, хранящей информацию о занесенных в нее мнимых точках
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{\rho}=\begin{Bmatrix} \rho&\rho&\cdots&\rho \end{Bmatrix}
Операции Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack \leftarrow x и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): x \leftarrow stack аналогичны операциям push и pop соответственно. Операция Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): x \Leftarrow stack копирует последний элемент стека в x без извлечения.
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_t',stack_{\rho}' - локальные переменные, аналогичные Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_t,stack_{\rho} , использующиеся во внутренних подциклах
Операция Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack' \leftarrow stack копирует переменную Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack в Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack'
Основное течение
- G.Множество контрольных точек()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ s_j \in
G.Множество первичных источников()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s'\leftarrow s_j
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{t}' \leftarrow t0_{mn} См. обсуждение к статье.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I \leftarrow 0
- Переход 1.1.8.1.4
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{t}' \leftarrow stack_{t}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{\rho}' \leftarrow stack_{\rho}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ f_m\in
G.Множество отражающих объектов()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho' \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho' .Построить зеркальное отображение(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} .Плоскость грани())
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{t}' \leftarrow t_{mn}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{\rho}' \leftarrow \rho'
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I' \leftarrow I
- Position Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Антенна().Позиция()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho' \leftarrow stack_{\rho}'
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} \leftarrow stack_{t}'
- Ray Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Луч().Создать(Position, Вектор(Position,Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho' .Позиция(), 1))
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I' > 0
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P\leftarrow Ray.Пересечение(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} .Плоскость грани())
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn}
.Принадлежность() Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \wedge
Расстояние(Position,Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho'
.Позиция()) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): >
Расстояние(Position,Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P
)
- Переход 1.1.8.1.11
- Иначе
- Переход 1.1.8.1.14
- Иначе
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P\leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho' .Позиция()
- Если IsShadowed(Ray, P, G)
- Переход 1.1.8.1.14
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I' > 0
- Angle Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \leftarrow Ray.Угол пересечения(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} .Плоскость грани())
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j \leftarrow Вторичный источник при рейтрейсинге.Создать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .НапряженностьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\omega_n,~\theta,~\varphi , Расстояние(Position,Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P ), G.Среда распространения()Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): ), Angle, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P,~t_{mn} )
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \theta, \varphi \leftarrow 0
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I' \leftarrow I'-1
- Переход 1.1.8.5
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho' .Зарегистрировать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .НапряженностьНевозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): (\omega_n,~\theta,~\varphi , Расстояние(Position, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho' .Позиция()), G.Среда распространения()Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): ) )
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E > E_{end}
См. обсуждение к статье.
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_t \leftarrow t_{m,n}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{\rho} \leftarrow \rho'
- Переход 1.1.6
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I \leftarrow I-1
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I > 0
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{m,n} \leftarrow stack_t
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho' \leftarrow stack_{\rho}
- Переход 1.1.8
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j \leftarrow s'
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ s_j \in
G.Множество первичных источников()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ \rho_k \in
G.Множество контрольных точек()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ s_j \in
G.Множество первичных источников()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ \omega_n \in
.Антенна().Тип антенны().Амплитудно-частотная характеристика()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Антенна().Позиция()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k .Позиция()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Ray\leftarrow Луч().Создать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P , Вектор(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p , 1))
- Если НЕ IsShadowed(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): Ray,p,
G)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k .Зарегистрировать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): s_j .Напряженность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_n,~p , G.Среда распространения()))
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I \leftarrow 1
- G.Множество отражающих объектов()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k .Построить зеркальное отображение(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} .Плоскость грани())
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_{\rho} \leftarrow \rho
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): stack_t \leftarrow t_{mn}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): [S,~B] \leftarrow Tracing(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): I,~stack_{\rho},~stack_t,~s_j,~\omega_n,~ G)
- Если Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): B
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S .Антенна().Позиция()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p \leftarrow Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k .Позиция()
- Луч().Создать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P , Вектор(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): p , 1))
- Если НЕ IsShadowed(G)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho_k .Зарегистрировать(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): S .Напряженность(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega_n,~p , G.Среда распространения()))
- Если НЕ IsEnd(Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): E,~I~,i
)
- NewLevel(Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): I,~stack_{\rho},~stack_t,~s_j,~\rho_k,~\omega_n,~ G)
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho \leftarrow stack_{\rho}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): t_{mn} \leftarrow stack_t
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ t_{mn} \in f_m
.Множество отражающих поверхностей()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ \omega_n \in
.Антенна().Тип антенны().Амплитудно-частотная характеристика()
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \forall ~ s_j \in
G.Множество первичных источников()
Возможности распараллеливания
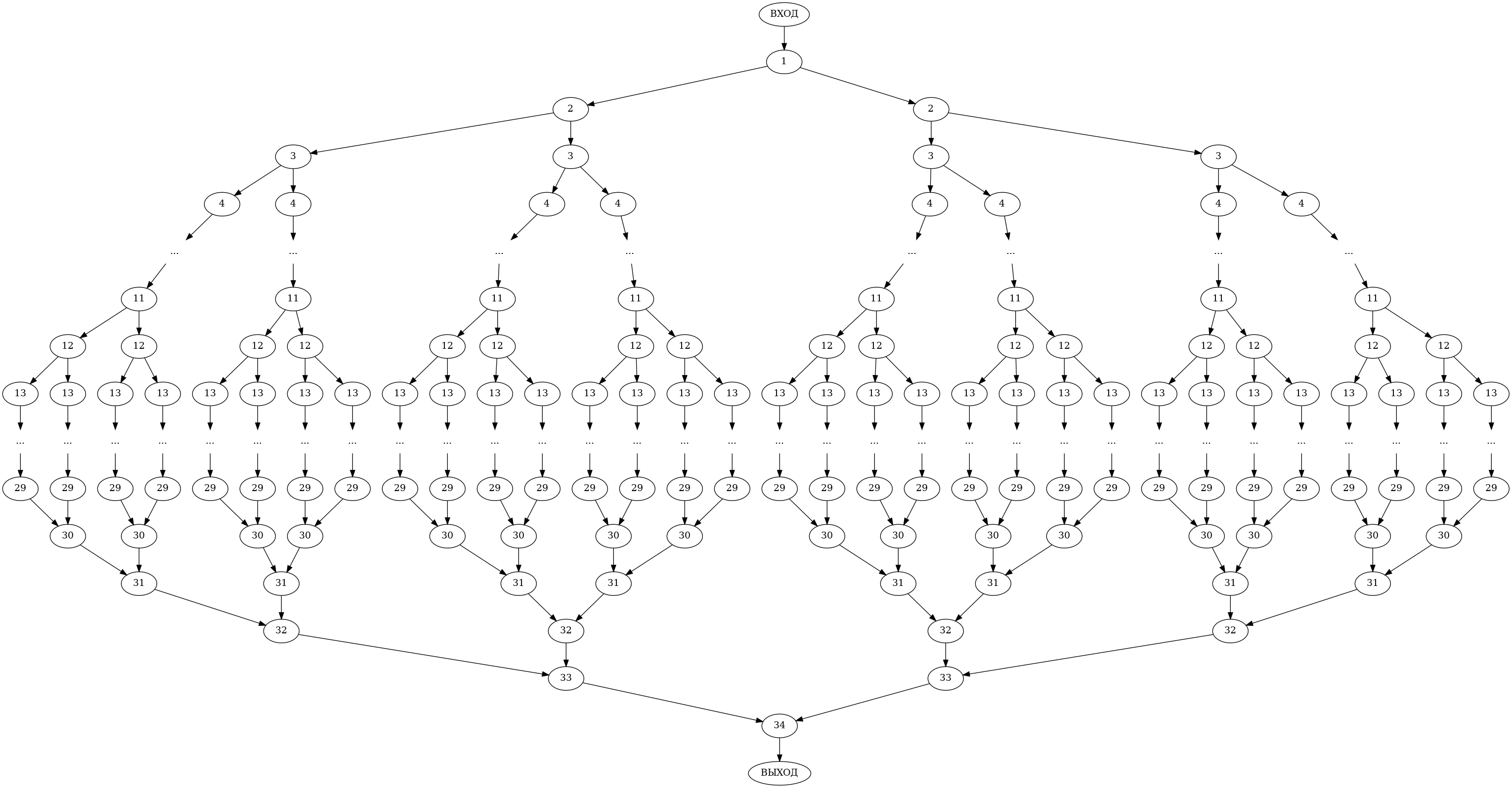
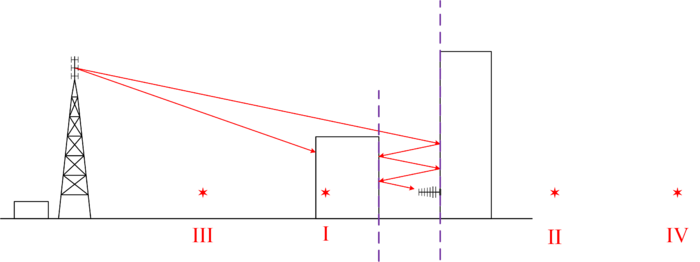

 )
)



 ) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \wedge
Расстояние(Position,Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho'
.Позиция()) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): >
Расстояние(Position,Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P
)
) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \wedge
Расстояние(Position,Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \rho'
.Позиция()) Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): >
Расстояние(Position,Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): P
)




