Распространение радиоволн ВЧ/Напряженность: различия между версиями
Nigiluk (обсуждение | вклад) |
Nigiluk (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
==<tt>Уменьшить по пробегу(Напряженность, Пробег, Погонное затухание)</tt>== | ==<tt>Уменьшить по пробегу(Напряженность, Пробег, Погонное затухание)</tt>== | ||
==<tt>Уменьшить по отражению(Напряженность, | ==<tt>Уменьшить по отражению(Напряженность, КДП_1*, КМП_1**, КДП_2, КМП_2, Угол, Вектор(Направление луча), Вектор(Нормаль грани))</tt>== | ||
<tt>*</tt> - комплексная диэлектрическая проницаемость, | |||
<tt>**</tt> - комплексная магнитная проницаемость. | |||
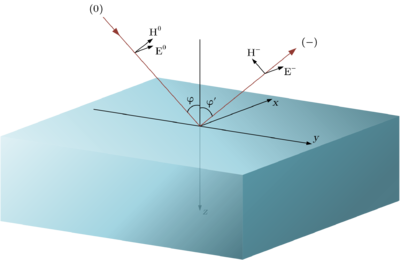
[[Файл:Ref Norm Pol.png|400px|thumb|right|Перпендикулярная поляризация]] | [[Файл:Ref Norm Pol.png|400px|thumb|right|Перпендикулярная поляризация]] | ||
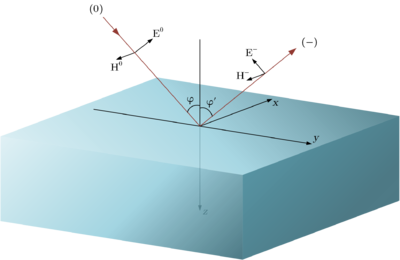
[[Файл:Ref Parall Pol.png|400px|thumb|right|Параллельная поляризация]] | [[Файл:Ref Parall Pol.png|400px|thumb|right|Параллельная поляризация]] | ||
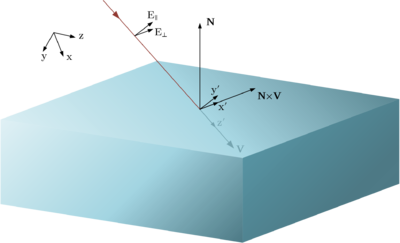
[[Файл:Ref_Rot_Axes.png|400px|thumb|right|Поворот координатных осей]] | |||
Пусть имеется граница раздела двух сред: | Пусть имеется граница раздела двух сред: | ||
:<math>\left \{ \dot \varepsilon_1,~\dot \mu_1,~\dot k_1,~\dot W_1 \right \},~z<0</math> | :<math>\left \{ \dot \varepsilon_1,~\dot \mu_1,~\dot k_1,~\dot W_1 \right \},~z<0</math> | ||
| Строка 38: | Строка 42: | ||
Таким образом отраженная волна имеет вид | Таким образом отраженная волна имеет вид | ||
<math>\vec {\dot E^-}=\vec {\dot E_{\bot}^-}+\vec {\dot E_{\|}^-}=\dot \rho_{\bot} \vec {\dot E_{\bot}^0}+\dot \rho_{\|} \vec {\dot E_{\|}^0}</math> | <math>\vec {\dot E^-}=\vec {\dot E_{\bot}^-}+\vec {\dot E_{\|}^-}=\dot \rho_{\bot} \vec {\dot E_{\bot}^0}+\dot \rho_{\|} \vec {\dot E_{\|}^0}</math> | ||
Т.к. напряженность поля дана в виде трехкомпонентного вектора относительно глобальной системы координат, необходимо найти параллельную и перпендикулярную составляющие соответственно данной грани и падающему лучу. Для этого составим матрицы поворота координатных осей таким образом, чтобы ось z совпала с направляющим вектором луча, а ось x с вектором векторного произведения направляющего вектора луча и вектора нормали грани. В результате в новых координатах <math>E_x=E_{\bot},~E_y=E_{\|},~E_z=0</math>. | |||
Версия 23:22, 26 мая 2017
Трехкомпонентный комплексный вектор
Функции
Уменьшить по пробегу(Напряженность, Пробег, Погонное затухание)
Уменьшить по отражению(Напряженность, КДП_1*, КМП_1**, КДП_2, КМП_2, Угол, Вектор(Направление луча), Вектор(Нормаль грани))
* - комплексная диэлектрическая проницаемость, ** - комплексная магнитная проницаемость.
Пусть имеется граница раздела двух сред:
- комплексная диэлектрическая проницаемость, где
- - диэлектрическая проницаемость среды,
- - проводимость среды
- - круговая частота волны
- магнитная проницаемость
При учете инерционности поляризации и намагничивания вводятся следующие комплексные проницаемости:
, где
- - угол диэлектрических потерь
- - угол магнитных потерь
- комплексное волновое число
- комплексное волновое сопротивление
Коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля):
, где
- - угол падения
Таким образом отраженная волна имеет вид
Т.к. напряженность поля дана в виде трехкомпонентного вектора относительно глобальной системы координат, необходимо найти параллельную и перпендикулярную составляющие соответственно данной грани и падающему лучу. Для этого составим матрицы поворота координатных осей таким образом, чтобы ось z совпала с направляющим вектором луча, а ось x с вектором векторного произведения направляющего вектора луча и вектора нормали грани. В результате в новых координатах .



 - комплексная диэлектрическая проницаемость, где
- комплексная диэлектрическая проницаемость, где
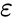 - диэлектрическая проницаемость среды,
- диэлектрическая проницаемость среды, - проводимость среды
- проводимость среды - круговая частота волны
- круговая частота волны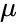 - магнитная проницаемость
- магнитная проницаемость

 , где
, где
 - угол диэлектрических потерь
- угол диэлектрических потерь - угол магнитных потерь
- угол магнитных потерь - комплексное волновое число
- комплексное волновое число
 - комплексное волновое сопротивление
- комплексное волновое сопротивление

 , где
, где
 - угол падения
- угол падения
 .
.