Распространение радиоволн ВЧ/Напряженность: различия между версиями
Nigiluk (обсуждение | вклад) |
Nigiluk (обсуждение | вклад) |
||
| Строка 31: | Строка 31: | ||
Коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля): | Коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля): | ||
<math>\dot \rho_{\bot} = \frac {\dot W_2 \cos \varphi - \dot W_1 \ | <math>\dot \rho_{\bot} = \frac {\dot W_2 \cos \varphi - \dot W_1 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi}} {\dot W_2 \cos \varphi + \dot W_1 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi}}</math> | ||
<math>\dot \rho_{\|} = \frac {\dot W_2 \ | <math>\dot \rho_{\|} = \frac {\dot W_2 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi} - \dot W_1 \cos \varphi} {\dot W_2 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi} + \dot W_1 \cos \varphi}</math>, где | ||
:<math>\varphi</math> - угол падения | :<math>\varphi</math> - угол падения | ||
Таким образом отраженная волна имеет вид | Таким образом отраженная волна имеет вид | ||
<math>\vec {\dot E}=\vec {\dot E_{\bot}}+\vec {\dot E_{\|}}</math> | <math>\vec {\dot E^-}=\vec {\dot E_{\bot}^-}+\vec {\dot E_{\|}^-}=\dot \rho_{\bot} \vec {\dot E_{\bot}^0}+\dot \rho_{\|} \vec {\dot E_{\|}^0}</math> | ||
Версия 22:07, 25 мая 2017
Трехкомпонентный комплексный вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\dot E} =\begin{pmatrix} \dot E_{x} \\ \dot E_{y} \\ \dot E_{z}\end{pmatrix}}
Функции
Уменьшить по пробегу(Напряженность, Пробег, Погонное затухание)
Уменьшить по отражению(Напряженность, Коэффициент преломления_1, Коэффициент преломления_2, Угол)
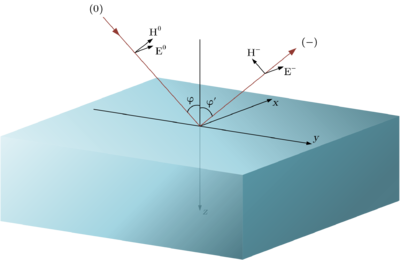
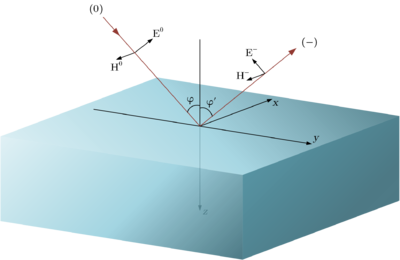
Пусть имеется граница раздела двух сред:
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left \{ \dot \varepsilon_1,~\dot \mu_1,~\dot k_1,~\dot W_1 \right \},~z<0}
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left \{ \dot \varepsilon_2,~\dot \mu_1,~\dot k_2,~\dot W_2 \right \},~z>0}
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \varepsilon = \varepsilon - i \frac{\sigma}{\omega}} - комплексная диэлектрическая проницаемость, где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon} - диэлектрическая проницаемость среды,
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \sigma - проводимость среды
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \omega - круговая частота волны
- магнитная проницаемость
При учете инерционности поляризации и намагничивания вводятся следующие комплексные проницаемости:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \mu = \mu \cos \beta - i \mu \sin \beta} , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \alpha - угол диэлектрических потерь
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \beta - угол магнитных потерь
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot k = \omega \sqrt{\dot \varepsilon \dot \mu}} - комплексное волновое число
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot W = \sqrt{\frac{\dot \mu}{\dot \varepsilon}}} - комплексное волновое сопротивление
Коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля):
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \rho_{\bot} = \frac {\dot W_2 \cos \varphi - \dot W_1 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi}} {\dot W_2 \cos \varphi + \dot W_1 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi}}}
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot \rho_{\|} = \frac {\dot W_2 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi} - \dot W_1 \cos \varphi} {\dot W_2 \sqrt{ 1 - \frac {\dot k_1^2} {\dot k_2^2} \sin^2 \varphi} + \dot W_1 \cos \varphi}} , где
- Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): \varphi - угол падения
Таким образом отраженная волна имеет вид Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec {\dot E^-}=\vec {\dot E_{\bot}^-}+\vec {\dot E_{\|}^-}=\dot \rho_{\bot} \vec {\dot E_{\bot}^0}+\dot \rho_{\|} \vec {\dot E_{\|}^0}}
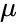 - магнитная проницаемость
- магнитная проницаемость
