Распространение радиоволн ВЧ/Напряженность: различия между версиями
Перейти к навигации
Перейти к поиску
Nigiluk (обсуждение | вклад) |
Nigiluk (обсуждение | вклад) |
||
| Строка 33: | Строка 33: | ||
<math>\dot \rho_{\bot} = \frac {\dot W_2 \cos \varphi - \dot W_1 \cos \vartheta} {\dot W_2 \cos \varphi + \dot W_1 \cos \vartheta}</math> | <math>\dot \rho_{\bot} = \frac {\dot W_2 \cos \varphi - \dot W_1 \cos \vartheta} {\dot W_2 \cos \varphi + \dot W_1 \cos \vartheta}</math> | ||
<math>\dot \rho_{\|} = \frac {\dot W_2 \cos \vartheta - \dot W_1 \cos \varphi} {\dot W_2 \cos \vartheta + \dot W_1 \cos \varphi}</math> | <math>\dot \rho_{\|} = \frac {\dot W_2 \cos \vartheta - \dot W_1 \cos \varphi} {\dot W_2 \cos \vartheta + \dot W_1 \cos \varphi}</math>, где | ||
:<math>\varphi</math> - угол падения | |||
:<math>\vartheta</math> - угол отражения | |||
Таким образом отраженная волна имеет вид | |||
<math>\vec {\dot E}=\vec {\dot E_{\bot}}+\vec {\dot E_{\|}}</math> | |||
Версия 21:37, 25 мая 2017
Трехкомпонентный комплексный вектор
Функции
Уменьшить по пробегу(Напряженность, Пробег, Погонное затухание)
Уменьшить по отражению(Напряженность, Коэффициент преломления_1, Коэффициент преломления_2, Угол)
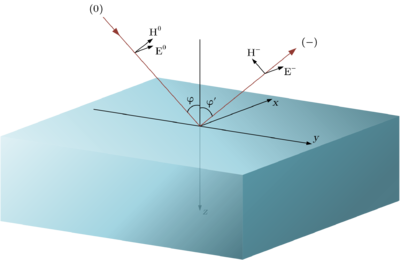
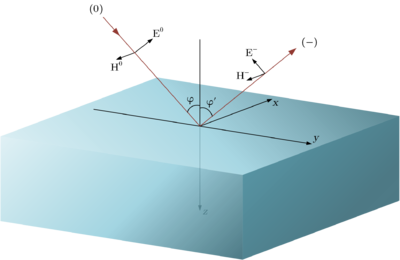
Пусть имеется граница раздела двух сред:
- комплексная диэлектрическая проницаемость, где
- - диэлектрическая проницаемость среды,
- - проводимость среды
- - круговая частота волны
- магнитная проницаемость
При учете инерционности поляризации и намагничивания вводятся следующие комплексные проницаемости:
, где
- - угол диэлектрических потерь
- - угол магнитных потерь
- комплексное волновое число
- комплексное волновое сопротивление
Коэффициенты отражения для перпендикулярной и параллельной поляризации имеют следующий вид (формулы Френеля):
, где
- - угол падения
- - угол отражения
Таким образом отраженная волна имеет вид



 - комплексная диэлектрическая проницаемость, где
- комплексная диэлектрическая проницаемость, где
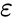 - диэлектрическая проницаемость среды,
- диэлектрическая проницаемость среды, - проводимость среды
- проводимость среды - круговая частота волны
- круговая частота волны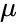 - магнитная проницаемость
- магнитная проницаемость

 , где
, где
 - угол диэлектрических потерь
- угол диэлектрических потерь - угол магнитных потерь
- угол магнитных потерь - комплексное волновое число
- комплексное волновое число
 - комплексное волновое сопротивление
- комплексное волновое сопротивление

 , где
, где
 - угол падения
- угол падения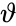 - угол отражения
- угол отражения